Производная. Непрерывность функции, имеющей производную Свойства функций, непрерывных на отрезке

Функция y=f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом, из дифференцируемости функции следует ее непрерывность.

Доказательство . Если, то

где б бесконечно малая величина, т.е. величина, стремящаяся к нулю при Дx>0. Но тогда

Дy=f "(x 0) Дx+бДx=> Дy>0 при Дx>0, т.е f(x) - f(x 0)>0 при x>x 0 ,

а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

В точке a при Дx>0 отношение не имеет предела (т.к. односторонние пределы различны при Дx>0-0 и Дx>0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Дx>0 отношение является знакопостоянной бесконечно большой величиной. Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки - "точка перегиба" c вертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип - "точка возврата" с вертикальной касательной - частный случай угловой точки.

1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке

Покажем, что она не имеет производной в этой точке.

f(0+Дx) = f(Дx) = |Дx|. Следовательно, Дy = f(Дx) - f(0) = |Дx|

Но тогда при Дx< 0 (т.е. при Дx стремящемся к 0 слева)

А при Дx > 0

Т.о., отношение при Дx> 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная "кривая" не имеет определенной касательной (в этой точке их две).

2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x= 0.

Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

Функция y = f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а ; b ] или интервала (а ; b ), то говорят, что она дифференцируема на отрезке [а ; b ] или соответственно в интервале (а ; b ).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y = f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом, из дифференцируемости функции следует ее непрерывность.

Доказательство . Если , то

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx →0. Но тогда

Δy =f "(x 0 ) Δx +αΔx => Δy →0 при Δx →0, т.е f(x) - f(x 0) →0 при x →x 0 , а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

В точке a при Δx →0 отношение не имеет предела (т.к. односторонние пределы различны при Δx →0-0 и Δx →0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Δx →0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки - "точка перегиба" c вертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип - "точка возврата" с вертикальной касательной - частный случай угловой точки.

Примеры.

1. Рассмотрим функцию y=|x| . Эта функция непрерывна в точке x = 0, т.к. .

Покажем, что она не имеет производной в этой точке.

f (0+Δx ) = f (Δx ) = |Δx |. Следовательно, Δy = f (Δx ) - f (0) = |Δx |

Но тогда при Δx < 0 (т.е. при Δx стремящемся к 0 слева)

А при Δx > 0

Т.о., отношение при Δx → 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x | в точке x = 0 не существует. Геометрически это значит, что в точке x = 0 данная "кривая" не имеет определенной касательной (в этой точке их две).

2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x = 0.

Следовательно, рассматриваемая функция не дифференцируема в точке x = 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy .

Производные элементарных функций.

1.
y = x n . Если n - целое положительное число, то, используя формулу бинома Ньютона:

(a + b ) n = a n +n·a n-1 ·b + 1/2?n(n - 1)a n-2 ?b 2 + 1/(2?3)?n(n - 1)(n - 2)a n-3 b 3 +…+ b n ,

можно доказать, что

Итак, если x получает приращение Δx , то f(x +Δx) = (x + Δx) n , и, следовательно,

Формулы 3 и 5 докажите самостоятельно.

Теорема. Если функция в некоторой точке x = x 0 имеет (конечную) производную , то

1) приращение функции может быть представлено в виде

или, короче, , где a есть величина, зависящая от Dx и вместе с ним стремящаяся к нулю, т.е. ;

2) функция в этой точке необходимо непрерывна.

Доказательство. 1) Согласно определению производной, . Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем

, где .

Определяя отсюда Dy , придем к формуле (3.6).

2) Чтобы доказать непрерывность функции, рассмотрим выражение (3.6). При Dx ®0 сумма в правой части (3.6) обращается в нуль. Следовательно, , или , а это означает, что функция в точке x 0 непрерывна.

Из доказанной теоремы следует, что функция, имеющая производную в данной точке, будет непрерывной в этой точке. Однако непрерывная в данной точке функция не всегда имеет производную в этой точке. Так, в точке x 0 = 1 функция y = |x – 1| является непрерывной, но производной в этой точке не имеет. Это означает, что данное условие является лишь необходимым.

Производная сложной функции

Теорема. Пусть 1) функция v = j (x ) имеет в некоторой точке x производную , 2) функция y = f (v ) имеет в соответствующей точке v производную Тогда сложная функция у = f (j (x )) в упомянутой точке х также будет иметь производную, равную произведению производных функций f (v ) и j (x ): [ f (j (x )) ]" = или короче

Доказательство. Придадим х произвольное приращение Δх ; пусть Δv – соответствующее приращение функции v = j (x ) и, наконец, Δу – приращение функции y = f (v ), вызванное приращением Δv . Воспользуемся соотношением (3.6), которое, заменяя x на v , перепишем в виде (a зависит от Δv и вместе с ним стремится к нулю). Разделив его почленно на Dx , получим

.

Если Dx устремить к нулю, то, согласно (3.6) (при условии, что у = v ), будет стремиться к нулю и Δv , а тогда, как мы знаем, будет также стремиться к нулю зависящая от Δv величина a . Следовательно, существует предел

который и представляет собой искомую производную .

Таким образом, производная сложной функции равна произведению производной внешней функции на производную внутренней функции.

Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила (3.7). Так, если у = f (u ), u = j (v ), v = y (x ), то

Примеры. 1. Пусть y = log a sin x ,иначе говоря, y = log a v , где v = sin x . По правилу (3.7)

2. , т.е. y= e u , u = v 2 , v = sin x. По правилу (3.8)

1.7. Производная показательно – степенной функции

Пусть u = u (x ) > 0 и v = v (x ) – функции, имеющие производные в фиксированной точке x . Найдем производную функции y = u v . Логарифмируя это равенство, получим: ln y = v ln u.

Продифференцируем обе части данного равенства по x :

.

Отсюда , или

Таким образом, производная показательно – степенной функции состоит из двух слагаемых: первое слагаемое получается, если при дифференцировании предположить, что и есть функция от х , а v есть постоянная (т.е. рассматривать u v как степенную функцию); второе слагаемое получается, если предположить, что v есть функция от х , а u = const (т.е. рассматривать u v как показательную функцию).

Примеры. 1. Если y = x tg x , то, полагая u = x , v = tg x ,согласно (3.9) имеем

= tg x x tg x – 1 + x tg x ln x sec 2 x .

Прием, примененный в данном случае для нахождения производной и состоящий в том, что сначала находят производную логарифма рассматриваемой функции, широко применяется при дифференцировании функций: при отыскании производной функции эти функции сначала логарифмируют, а затем из равенства, полученного после дифференцирования логарифма функции, определяют производную функции. Такая операция называется логарифмическим дифференцированием.

2.Требуется найти производную от функции

.

Логарифмируя, находим:

ln y = 2ln(x + 1) + ln(x – 1) – 3 ln(x + 4) – x.

Дифференцируем обе части последнего равенства:

.

Умножая на у и подставляя вместо у , получаем.

3 Определение производной функции в точке Пусть функция f(x) определена в некоторой окрестности точки x 0. ОПРЕДЕЛЕНИЕ. Если существует (конечный) предел отношения то f(x) называется дифференцируемой точке х 0, а сам предел называется производной функции f(x) в точке х 0 и обозначается f "(x 0), то есть Обозначим x = x – x 0 – приращение аргумента при переходе из точки х 0 в точку х, а y = f(x 0 + x) – f(x 0) – соответствующее приращение функции. Тогда производная функции f(x) в точке х 0 предел отношения приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю.

4 Пример 1. Приведем примеры вычисления производных некоторых простейших элементарных функций, исходя из определения производной. y = a x (0 0.Считая, что | х | 0 – произвольная точка, то 0.Считая, что | х | 0 – произвольная точка, то">

0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R." title="5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R." class="link_thumb"> 5 5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R. 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R."> 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R."> 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R." title="5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R."> title="5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R.">

6 ТЕОРЕМА. Если функция f(x) дифференцируема в точке x 0, то она непрерывна в этой точке. Доказательство. Пусть существует Тогда Отсюда получим, что f (x) – f (x 0) = f "(x 0) (х – х 0) + (х – х 0)α(x) при х х 0. То есть f(x) непрерывна в точке x 0. Непрерывность дифференцируемой функции (1)

7 ЗАМЕЧАНИЕ. Непрерывность функции в точке не является достаточным условием существования в этой точке производной. Пример 5. f (x) = х. Исследуем поведение f (x) в окрестности х 0 = 0. Здесь и f (x) f (0) = 0 при x 0. Т.е. функция непрерывна в точке х 0 = 0. Рассмотрим x y 0 Предел не существует, так как Итак, функция f (x) = х не имеет производной в точке х = 0, хотя непрерывна в этой точке

8 Пример x y 0 при х 0. при х 0. Т.е. f(x) непрерывна в точке х = 0. Т.е. f(x) не имеет производной в точке х = 0 и, следовательно, не дифференцируема в этой точке. Исследуем поведение f (x) в окрестности точки х = 0.

9 Пусть функция у = f(x) дифференцируема в точке х 0. Тогда, согласно (1), ее приращение в точке х 0 можно записать в виде y = f(x 0 + x) – f(x 0) = f (x 0) х + о(x) при х. Дифференциал функции f (x 0) x – главная линейная относительно x часть приращения функции у = f(x) в точке х 0 называется дифференциалом функции в точке х 0 при приращении x и обозначается df(х 0 ; x) или df(х 0) или df или dу. y = f(x 0 + x) – f(x 0) = df(х 0 ; x) + о(x) при х. ОПРЕДЕЛЕНИЕ. Главная часть приращения, линейная относительно х. Бесконечно малая более высокого порядка, чем х. Теперь приращение функции можно записать так:

10 ЗАМЕЧАНИЕ. Приращение х часто обозначают символом dх и называют дифференциалом независимой переменной. Таким образом, дифференциал функции в точке x 0 можно записать в виде df(х 0) = f "(x 0) dх. Если функция дифференцируема в каждой точке некоторого интервала, то ее дифференциал dy – функция от х и dx: dy = f "(x) dx. Отсюда, в частности, получается выражение для производной То есть производную можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.

11 Геометрический смысл производной и дифференциала Пусть функция у = f(x) определена в U(x 0) и дифференцируема в точке х 0. М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + у 0 L – секущая L 0 – касательная x y = f(x 0 + x) – f(x 0) при х в силу непрерывности функции. Касательной к графику функции у = f(x) в точке М 0 называется предельное положение секущей L при х. y Если функция дифференцируема в точке х 0, то в уравнении секущей у/ х f (x 0) при х и уравнение касательной имеет вид у = у 0 + f (x 0) (х – х 0).

12 М0М0 М x0x0 x 0 + x dy = df(х 0 ; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o(x) при x 0 L0L0 tg = f (x 0) Если же у/ х при х, то прямая х = х 0, получающаяся из уравнения секущей, называется вертикальной касательной к графику функции в точке М 0. Из уравнения касательной получим у – у 0 = f (x 0) (х – х 0) = df(х 0) – приращение ординаты касательной при переходе из точки х 0 в точку х. Нормалью к графику функции в точке М 0 называется прямая, перпендикулярная касательной, проходящая через точку М 0. Ее уравнение имеет вид у = у 0 – 1/f (x 0) (х – х 0). L 1 – нормаль

13 Физические приложения производной и дифференциала Если S(t) – путь, пройденный материальной точкой за время t, то S "(t) – мгновенная скорость материальной точки, а dS = S "(t)dt – расстояние, которое прошла бы материальная точка за промежуток времени от t до t + dt, если бы она двигалась со скоростью, равной мгновенной скорости в момент t. Если Q(t) – количество электричества, протекающего через поперечное сечение проводника в момент времени t, то Q "(t) = I – сила тока. Если N(t) – количество вещества, образующегося в момент t в ходе химической реакции, то N "(t) – скорость химической реакции.

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a , b ], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b , непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a , b ], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a , b ], то найдётся хотя бы одна точка x 1 Î [a , b ] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x 1) ≥ f(x) . Аналогично найдётся такая точка x 2 , в которой значение функции будет самым маленьким из всех значений на отрезке: f(x 1) ≤ f(x) .

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x 2 и x 2 ".

Замечание . Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a , b ). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a , b ], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a , b ] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка найдется, по крайней мере, одна точка x = C , в которой функция обращается в ноль: f(C) = 0, где a < C< b

Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x) , соответствующие концам отрезка [a , b ] лежат по разные стороны от оси Ox , то этот график хотя бы в одной точке отрезка пересекает ось Ox . Разрывные функции этим свойством могут не обладать.

Эта теорема допускает следующее обобщение.

Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a , b ] и f(a) = A , f(b) = B . Тогда для любого числа C , заключённого между A и B , найдётся внутри этого отрезка такая точка C Î [a , b ], что f(c) = C .

Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x) . Пусть f(a) = A , f(b) = B . Тогда любая прямая y = C , где C – любое число, заключённое между A и B , пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C , при котором f(c) = C .

Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности:

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента x из этого промежутка функция y=f(x) имеет определенное значение.

Рассмотрим два значения аргумента: исходное x 0 и новое x .

Разность x– x 0 называется приращением аргумента x в точке x 0 и обозначается Δx . Таким образом, Δx = x – x 0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x 0 +Δx , т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x 0 значение функции было f(x 0 ), то в новой точке x функция будет принимать значение f(x) = f(x 0 +Δx) .

Разность y – y 0 = f(x) – f(x 0 ) называется приращением функции y = f(x) в точке x 0 и обозначается символом Δy . Таким образом,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Обычно исходное значение аргумента x 0 считается фиксированным, а новое значение x – переменным. Тогда y 0 = f(x 0 ) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δx также будут переменными и формула (1) показывает, что Dy является функцией переменной Δx .

Составим отношение приращения функции к приращению аргумента

Найдем предел этого отношения при Δx →0. Если этот предел существует, то его называют производной данной функции f(x) в точке x 0 и обозначают f "(x 0). Итак,

Производной данной функции y = f(x) в точке x 0 называется предел отношения приращения функции Δy к приращению аргумента Δx , когда последнее произвольным образом стремится к нулю.

Заметим, что для одной и той же функции производная в различных точках x может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x . Эта функция обозначается f "(x )

Производная обозначается символами f "(x),y ", . Конкретное значение производной при x = a обозначается f "(a ) или y "| x=a .

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Для непосредственного нахождения производной по определению можно применить следующее практическое правило :

Примеры.

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t , где s – путь, пройденный к моменту времени t , v – скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние s будет зависеть от времени t , т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t 0 . К этому моменту точка прошла путь s=s(t 0 ). Определим скорость v материальной точки в момент времени t 0 .

Для этого рассмотрим какой-нибудь другой момент времени t 0 + Δt . Ему соответствует пройденный путь s=s(t 0 + Δt ). Тогда за промежуток времени Δt точка прошла путь Δs=s(t 0 + Δt) –s(t).

Рассмотрим отношение . Оно называется средней скоростью в промежутке времени Δt . Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t 0 (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt .

Итак, скоростью движения в данный момент времени t 0 (мгновенной скоростью) называется предел средней скорости в промежутке от t 0 до t 0 +Δt , когда Δt →0:

,

т.е. скорость неравномерного движения это производная от пройденного пути по времени.

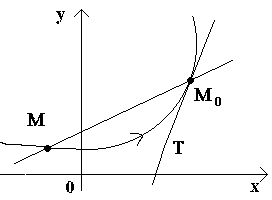
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М 0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M 0 M . Если точка М начинает перемещаться по кривой, а точка М 0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М 0 с любой стороны секущая стремится занять положение определенной прямой М 0 Т , то прямая М 0 Т называется касательной к кривой в данной точке М 0 .

Т.о., касательной к кривой в данной точке М 0 называется предельное положение секущей М 0 М , когда точка М стремится вдоль кривой к точке М 0 .

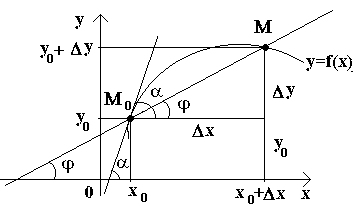
Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х 0 функция принимает значение y 0 =f(x 0). Этим значениям x 0 и y 0 на кривой соответствует точка М 0 (x 0 ; y 0). Дадим аргументу x 0 приращение Δх . Новому значению аргумента соответствует наращенное значение функции y 0 +Δ y=f(x 0 –Δx) . Получаем точку М(x 0 +Δx ; y 0 +Δy). Проведем секущую М 0 М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox . Составим отношение и заметим, что .

Если теперь Δx →0, то в силу непрерывности функции Δу →0, и поэтому точка М , перемещаясь по кривой, неограниченно приближается к точке М 0 . Тогда секущая М 0 М будет стремиться занять положение касательной к кривой в точке М 0 , а угол φ→α при Δx →0, где через α обозначили угол между касательной и положительным направлением оси Ox . Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

т.е. f "(x) = tg α .

Т.о., геометрически у "(x 0) представляет угловой коэффициент касательной к графику этой функции в точке x 0 , т.е. при данном значении аргумента x , производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М 0 (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х 2 в точке М (-1; 1).

Ранее мы уже видели, что (x 2)" = 2х . Но угловой коэффициент касательной к кривой есть tg α = y "| x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а ; b ] или интервала (а ; b ), то говорят, что она дифференцируема на отрезке [а ; b ] или соответственно в интервале (а ; b ).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство . Если , то

,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx →0. Но тогда

Δy =f "(x 0 ) Δx +αΔx => Δy →0 при Δx →0, т.е f(x) – f(x 0) →0 при x →x 0 , а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

В точке a при Δx →0 отношение не имеет предела (т.к. односторонние пределы различны при Δx →0–0 и Δx →0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Δx →0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.