Linear difference equations solving difference equations. Difference equation

Equation of the form

where some numbers are called a linear difference equation with constant coefficients.

Usually, instead of equation (1), an equation is considered that is obtained from (1) by passing from finite differences to the value of the function, i.e., an equation of the form

If there is a function in equation (2), then such an equation is called homogeneous.

Consider the homogeneous equation

The theory of linear difference equations is similar to the theory of linear differential equations.

Theorem 1.

If the functions are solutions to the homogeneous equation (3), then the function

is also a solution to equation (3).

Proof.

Let's substitute the functions in (3)

since the function is a solution to equation (3).

Lattice functions are called linearly dependent if there are numbers such that and at least one is different from zero, for any n the following is true:

(4)

If (4) occurs only when then the functions are called linearly independent.

Any k linearly independent solutions to equation (3) form a fundamental system of solutions.

Let linearly independent solutions to equation (3), then

is a general solution to equation (3). When a specific condition is found, it is determined from the initial conditions

We will look for a solution to equation (3) in the form:

Let's substitute into equation (3)

Let's divide equation (5) by

Characteristic equation. (6)

Let us assume that (6) has only simple roots It is easy to verify that are linearly independent. The general solution of the homogeneous equation (3) has the form

Example.

Consider the equation

The characteristic equation has the form

The solution has the form

Let the root have multiplicity r. This root corresponds to the solution

If we assume that the remaining roots are not multiples, then general solution equation (3) has the form

Let's consider the general solution inhomogeneous equation (2).

A particular solution to the inhomogeneous equation (2), then the general solution

LECTURE 16

Lecture outline

1. The concept of D and Z - transformations.

2. Scope of application of D and Z - transformations.

3. Inverse D and Z transformations.

DISCRETE LAPLACE TRANSFORM.

Z – CONVERSION.

IN applied research associated with the use of lattice functions, the discrete Laplace transform (D - transform) and Z - transform are widely used. By analogy with the usual Laplace transform, the discrete transform is given in the form

where (1)

Symbolically, D - the transformation is written in the form

For offset trellis functions

where is the offset.

Z – transformation is obtained from D – transformation by substitution and is given by the relation

(3)

For a shifted function

A function is called original if

2) there is a growth indicator, i.e. there are such and that

(4)

The smallest number (or the limit to which the smallest number tends) for which inequality (4) is true is called the abscissa of absolute convergence and is denoted

Theorem.

If the function is original, then the image is defined in the domain Re p > and is an analytic function in this domain.

Let us show that for Re p > series (1) converges absolutely. We have

since the indicated amount is the sum of the terms of a decreasing geometric progression with the indicator It is known that such a progression converges. The value can be taken to be arbitrarily close to the value , i.e., the first part of the theorem is proven.

We accept the second part of the theorem without proof.

The image is periodic function with imaginary period

When studying an image, there is no point in considering it on the entire complex plane; it is enough to limit the study to any strip of width. Usually, a strip is used on the complex plane, which is called the main one. That. We can assume that the images are defined in the half-strip

and is an analytic function in this half-strip.

Let us find the domain of definition and analyticity of the function F(z) by setting . Let us show that the semi-strip plane p is transformed by transformation into a region on the z plane: .

Indeed, the segment , limiting the semi-strip on the plane p, is translated on the plane z into the neighborhood: .

Let us denote by the line into which the transformation takes the segment . Then

Neighborhood.

That. Z – transformation F(z) is defined in the domain and is an analytical function in this domain.

The inverse D transformation allows one to reconstruct the lattice function from the image

(5)

Let us prove the validity of the equality.

Lie inside the neighborhood.

(7)

(8)

In equalities (7) and (8), residues are taken over all singular points of the function F(s).

Introduction

In recent decades, mathematical methods have increasingly penetrated the humanities and, in particular, economics. Thanks to mathematics and its effective application one can hope for economic growth and prosperity of the state. Effective, optimal development is impossible without the use of mathematics.

The purpose of this work is to study the application of difference equations in the economic sphere of society.

This work has the following tasks: defining the concept of difference equations; consideration of linear difference equations of the first and second order and their application in economics.

When working on the course project, materials available for study were used teaching aids on economics, mathematical analysis, works of leading economists and mathematicians, reference publications, scientific and analytical articles published in Internet publications.

Difference equations

§1. Basic concepts and examples of difference equations

Difference equations play big role V economic theory. Many economic laws are proven using these exact equations. Let's look at the basic concepts of difference equations.

Let time t act as the independent variable, and the dependent variable is defined for time t, t-1, t-2, etc.

Let us denote by the value at time t; through - the value of the function at a moment shifted back by one (for example, in the previous hour, in the previous week, etc.); through - the value of the function y at the moment shifted back two units, etc.

Equation

where are constants, is called an n-th order inhomogeneous difference equation with constant coefficients.

Equation

In which =0 is called a homogeneous difference equation of the nth order with constant coefficients. To solve an nth order difference equation means to find a function that turns this equation into the correct identity.

A solution in which there is no arbitrary constant is called a partial solution of a difference equation; if the solution contains an arbitrary constant, then it is called a general solution. The following theorems can be proven.

Theorem 1. If the homogeneous difference equation (2) has solutions and, then the function will also be a solution

where and are arbitrary constants.

Theorem 2. If is a particular solution of the inhomogeneous difference equation (1) and is the general solution of the homogeneous equation (2), then the general solution of the inhomogeneous equation (1) will be the function

Arbitrary constants. These theorems are similar to those for differential equations. A system of linear difference equations of the first order with constant coefficients is a system of the form

where is a vector of unknown functions, is a vector of known functions.

There is a matrix of size nn.

This system can be solved by reducing it to an nth order difference equation by analogy with solving a system of differential equations.

§ 2. Solution of difference equations

Solution of a first order difference equation. Consider the inhomogeneous difference equation

The corresponding homogeneous equation is

Let's check if the function will be

solving equation (3).

Substituting into equation (4), we get

Therefore, there is a solution to equation (4).

The general solution to equation (4) is the function

where C is an arbitrary constant.

Let be a particular solution of the inhomogeneous equation (3). Then the general solution to difference equation (3) is the function

Let's find a particular solution to the difference equation (3) if f(t)=c, where c is some variable.

We will look for a solution in the form of a constant m. We have

Substituting these constants into the equation

we get

Therefore, the general solution to the difference equation

Example1. Using a difference equation, find the formula for the increase in cash deposit A ​​in the savings bank, deposited at p% per annum.

Solution. If a certain amount is deposited in a bank at a compound interest p, then by the end of the year t its amount will be

This is a first order homogeneous difference equation. His decision

where C is some constant that can be calculated from the initial conditions.

If we accept, then C=A, whence

This is a well-known formula for calculating the growth of a cash deposit placed in a savings bank at a compound interest rate.

Solution of a second order difference equation. Let us consider a second-order inhomogeneous difference equation

and the corresponding homogeneous equation

If k is the root of the equation

is a solution to homogeneous equation (6).

Indeed, substituting into the left side of equation (6) and taking into account (7), we obtain

Thus, if k is the root of equation (7), then it is a solution to equation (6). Equation (7) is called the characteristic equation for equation (6). If the discriminant characteristic equation (7) is greater than zero, then equation (7) has two different real roots and, and the general solution of the homogeneous equation (6) has the following form.

Security questions:

1. What function is called a grid function?

2. Which equation is called a difference equation?

3. What equations are called 1st order difference equations?

4. How to find the general solution of a 1st order inhomogeneous difference equation?

5. Which solution to the difference equation is called fundamental?

6. Why does the general solution of a homogeneous equation with constant coefficients have the form of a geometric progression?

Assignments.

1. Write a procedure for solving a first-order difference equation with the initial condition.

2. For given equation find general and particular solutions analytically.

3. Compare the results of calculations using the recurrent formula with the analytical solution.

4. Find out how disturbance affects the result initial condition, coefficients of the equation, right side.

				Directions

Let's find the general solution to the 1st order difference equation

. (1)

We obtain a partial solution of the homogeneous equation for using the recurrent formula: . Since the Y value doubles at each subsequent grid point, we get geometric progression with denominator q=2:

We find a particular solution to the inhomogeneous equation in the form: , where A is an undetermined coefficient. Then , , and, equating the resulting value to the given right-hand side, we find the undetermined coefficient A=. Finally, the general solution is: .

Using the initial condition, we find the constant: . Finally, a particular solution for a given initial condition:

.

To study the stability of the solution to perturbation of the solution itself and the initial condition, consider the following equation:

with perturbed initial condition

(here is the magnitude of the disturbance). Subtracting the original equation (1), we obtain the difference equation for the disturbance:

with the initial condition. The solution to this equation is: , i.e. even a small disturbance at any node grows exponentially with increasing node number.

The student needs to illustrate the above: explore the influence of perturbations of the initial condition, right-hand sides and coefficients of the equation by changing the recurrence formula.

The option, in accordance with the student number on the list in the journal, must be solved in the programming language C++ (use of the Builder environment is allowed) or Pascal (use of the Delphi environment is allowed).

1. Recurrent formula for obtaining a numerical solution.
2. Analytical solution of the difference equation. A general solution and a particular solution that satisfies the given initial conditions.
3. Investigate the stability of the solution to perturbations of the initial condition and the solution analytically.

b) when the coefficients of the equation are perturbed;

c) when the right side is perturbed.

Topic: 2nd order difference equations

Security questions:

1. What equations are called 2nd order difference equations?

2. What is a characteristic equation?

3. What does a particular solution of a 2nd order homogeneous difference equation with real roots of the characteristic equation look like?

4. What does a particular solution of a 2nd order homogeneous difference equation with complex roots of the characteristic equation look like?

5. How to find the general solution of a 2nd order inhomogeneous difference equation?

6. What is a numerical and analytical solution to a 2nd order difference equation?

7. What problems are called well-conditioned?

Quests

1. Write a procedure for solving a difference boundary value problem for a second-order equation with boundary conditions , .

2. For a given equation, find the general and particular solutions analytically and check the conditionality criterion.

3. Compare the results of calculations using the recurrent formula with the analytical solution.

4. Find out how perturbation of the boundary conditions and the right-hand side affects the result.

						Let's find a general solution to the 2nd order difference equation can be found by choosing arbitrary constants. Along with Cauchy problems, two-point boundary value problems are also considered for second-order equations, in which the values ​​of the grid function are specified at two nodes located not in a row, but at the ends of a certain finite segment: (boundary conditions ). An analytical solution to such a problem can be obtained by a suitable choice of arbitrary constants in the general solution. However, unlike a problem with initial conditions, a boundary value problem will not necessarily be uniquely solvable. That's why great value has the clarification of a class of boundary value problems that have unique solvability and weak sensitivity to perturbation (due to rounding errors) of the right-hand sides and boundary conditions. We will call such problems well conditioned Let us consider an example of an ill-conditioned boundary value problem Statement of the problem. Initial difference equation and boundary conditions. Procedure for obtaining a numerical solution. Analytical solution of a difference boundary value problem. A general solution and a particular solution that satisfies the given boundary conditions. Checking the conditionality criterion. Graphs of the numerical solution and analytical solution (on the same axes). Graph of the difference between the numerical and analytical solution. Graphs of the outraged numerical solutions and the difference between the perturbed and unperturbed solutions: a) when the initial condition is perturbed; b) when the right side is perturbed. Conclusion about the conditionality of the boundary value problem.

Solving ordinary linear difference equations

with constant coefficients

The relationship between the output and input of a linear discrete system can be described by an ordinary linear difference equation with constant coefficients

,

Where y[n]- output signal at the moment n,

x[n]- input signal at the moment n,

a i,b k– constant coefficients.

Two methods can be used to solve such equations

• Direct method
• Method Z – transformations.

First, let's consider solving a linear difference equation using the direct method.

The general solution of a non-homogeneous (with a non-zero right-hand side) linear difference equation is equal to the sum of general solution linear homogeneous difference equation and private solution inhomogeneous equation

The general solution of the homogeneous difference equation ( zero-inputresponse) y h [n]

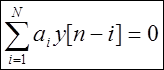
is defined as

.

Substituting this solution into a homogeneous equation, we obtain

Such a polynomial is called characteristic polynomial systems. He has N roots . The roots can be real or complex and some roots can be coincident (multiple).

If the roots are real and different, then the solution to the homogeneous equation has the form

where are the coefficients

If some root, for example, λ 1 has a multiplicity m, then the corresponding solution term takes the form

If all coefficients of a homogeneous equation and, accordingly, a characteristic polynomial are real, then the two terms of the solution corresponding to simple complex conjugate roots can be represented (written) in the form , with the coefficients A,B are determined by initial conditions.

Type of private solution y p [n] equation depends on the right side (input signal) and is determined according to the table below

Table 1. Type of particular solution for different character of the right side

Input signalx[n]	Private solutiony p [n]
A(constant)

The solution of a linear difference equation by the Z - transformation method consists in using Z– transformations to an equation using the properties of linearity and time shift. The result is a linear algebraic equation relatively Z- images of the required function. Reverse Z– the transformation gives the desired solution in the time domain. To obtain the inverse Z - transformation, the decomposition is most often used rational expression to simple (elementary) fractions, since the inverse transformation from a separate elementary fraction has a simple form.

Note that to move to the time domain, other methods for calculating the inverse Z-transform can be used.

Example. Let us determine the response (output signal) of the system described by the linear difference equation to the input signal

Solution.

1. Direct method for solving the equation.

Homogeneous equation. Its characteristic polynomial.

Roots of a polynomial .

Solution of a homogeneous equation.

Since, we define a particular solution in the form .

We substitute it into the equation

To find the constant TO let's accept n=2. Then

Or, K=2.33

Hence the particular solution and the general solution to the difference equation (1)

Let's find the constants C 1 And C 2. To do this, let's put n=0, then from the original difference equation we obtain . For a given equation

That's why . From expression (1)

Hence,

.

From expression (1) for n=1 we have .
We obtain the following two equations for C 1 and C 2

.

Solving this system gives the following values: C 1 = 0.486 and C 2 = -0.816.

Therefore, the general solution to this equation is

2. Solution using the Z – transformation method.

Let's take Z - transformation from the original difference equation, taking into account the property (theorem) of the time shift 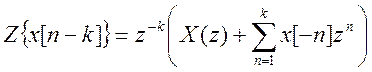. We get

The use of equations is widespread in our lives. They are used in many calculations, construction of structures and even sports. Man used equations in ancient times, and since then their use has only increased. A difference equation is an equation that connects the value of some unknown function at any point with its value at one or more points located at a certain interval from the given one. Example:

\[Г (z+1) = zГ(z)\]

For difference equations with constant coefficients, there are detailed methods for finding a solution in closed form. Inhomogeneous and homogeneous difference equations of the nth order are given, respectively, by equations where \ are constant coefficients.

Homogeneous difference equations.

Consider the nth order equation

\[(a_nE^n +a(n-1)E^n1 + \cdots +a_1E + a_1)y(k) = 0 \]

The proposed solution should be sought in the form:

where \ is a constant value to be determined. The type of proposed solution given by the equation is not the most common. Valid values\ serve as the roots of the polynomial in \[ e^r.\] When\[ \beta = e^r \]the expected solution becomes:

where \[\beta\] is a constant value to be determined. Substituting the equation and taking into account \, we obtain the following characteristic equation:

Inhomogeneous difference equations. Method of undetermined coefficients. Let us consider the difference equation of the nth order

\[ (a_nEn +a_(n-1)En^-1+\cdots+ a_1E +a_1)y(k) =F(k) \]

The answer looks like this:

Where can I solve difference equations online?

You can solve the equation on our website https://site. The free online solver will allow you to solve online equations of any complexity in a matter of seconds. All you need to do is simply enter your data into the solver. You can also watch video instructions and learn how to solve the equation on our website. And if you still have questions, you can ask them in our VKontakte group http://vk.com/pocketteacher. Join our group, we are always happy to help you.