What does decimal mean? Decimals
In this article we will understand what a decimal fraction is, what features and properties it has. Go! 🙂
A decimal fraction is a special case of ordinary fractions (where the denominator is a multiple of 10).
Definition
Decimals are fractions whose denominators are numbers consisting of one and a number of zeros following it. That is, these are fractions with a denominator of 10, 100, 1000, etc. Otherwise, a decimal fraction can be characterized as a fraction with a denominator of 10 or one of the powers of ten.
Examples of fractions:
, ,
Decimal fractions are written differently than ordinary fractions. Operations with these fractions are also different from operations with ordinary ones. The rules for operations with them are largely similar to the rules for operations with integers. This, in particular, explains their demand for solving practical problems.
Representation of fractions in decimal notation
The decimal fraction does not have a denominator; it displays the number of the numerator. IN general view The decimal fraction is written according to the following scheme:
where X is the integer part of the fraction, Y is its fractional part, “,” is the decimal point.
To correctly represent a common fraction as a decimal, it must be regular, that is, with a highlighted whole part(if possible) and a numerator that is less than the denominator. Then in decimal notation the integer part is written before the decimal point (X), and the numerator of the common fraction is written after the decimal point (Y).
If the numerator contains a number with fewer digits than the number of zeros in the denominator, then in part Y the missing number of digits in the decimal notation is filled with zeros ahead of the numerator digits.
Example: ![]()
If common fraction less than 1, i.e. does not have an integer part, then for X in decimal form write 0.
In the fractional part (Y), after the last significant (non-zero) digit, an arbitrary number of zeros can be entered. This does not affect the value of the fraction. Conversely, all zeros at the end of the fractional part of the decimal can be omitted.
Reading Decimals
Part X is generally read as follows: “X integers.”
The Y part is read according to the number in the denominator. For denominator 10 you should read: “Y tenths”, for denominator 100: “Y hundredths”, for denominator 1000: “Y thousandths” and so on... 😉
Another approach to reading, based on counting the number of digits of the fractional part, is considered more correct. To do this, you need to understand that the fractional digits are located in a mirror image with respect to the digits of the whole part of the fraction.
The names for correct reading are given in the table:

Based on this, reading should be based on compliance with the name of the digit of the last digit of the fractional part.
- 3.5 reads "three point five"
- 0.016 reads "zero point sixteen thousandths"
Converting an arbitrary fraction to a decimal
If the denominator of a common fraction is 10 or some power of ten, then the conversion of the fraction is performed as described above. In other situations, additional transformations are required.
There are 2 translation methods.
First transfer method
The numerator and denominator must be multiplied by such an integer that the denominator produces the number 10 or one of the powers of ten. And then the fraction is represented in decimal notation.
This method is applicable for fractions whose denominator can only be expanded into 2 and 5. So, in the previous example ![]() . If the expansion contains other prime factors (for example, ), then you will have to resort to the 2nd method.
. If the expansion contains other prime factors (for example, ), then you will have to resort to the 2nd method.
Second translation method
The 2nd method is to divide the numerator by the denominator in a column or on a calculator. The whole part, if any, does not participate in the transformation.
The rule for long division that results in a decimal fraction is described below (see Division of decimals).
Converting a decimal fraction to a common fraction
To do this, you should write down its fractional part (to the right of the decimal point) as the numerator, and the result of reading the fractional part as the corresponding number in the denominator. Next, if possible, you need to reduce the resulting fraction.
![]()
Finite and infinite decimal fraction
A decimal fraction is called a final fraction, the fractional part of which consists of a finite number of digits.
All the examples above contain final decimal fractions. However, not every ordinary fraction can be represented as a final decimal. If the 1st conversion method is not applicable for a given fraction, and the 2nd method demonstrates that the division cannot be completed, then only an infinite decimal fraction can be obtained.
In full form infinite fraction impossible to record. In incomplete form, such fractions can be represented:
- as a result of reduction to the desired number of decimal places;
- as a periodic fraction.
A fraction is called periodic if after the decimal point it is possible to distinguish an endlessly repeating sequence of digits.
The remaining fractions are called non-periodic. For non-periodic fractions, only the 1st method of representation (rounding) is allowed.
An example of a periodic fraction: 0.8888888... Here there is a repeating number 8, which, obviously, will be repeated ad infinitum, since there is no reason to assume otherwise. This figure is called period of the fraction.
Periodic fractions can be pure or mixed. A pure decimal fraction is one whose period begins immediately after the decimal point. A mixed fraction has 1 or more digits before the decimal point.
54.33333… – periodic pure decimal fraction
2.5621212121… – periodic mixed fraction
Examples of writing infinite decimal fractions:
The 2nd example shows how to correctly format a period in writing a periodic fraction.
Converting periodic decimal fractions to ordinary fractions
To convert a pure periodic fraction into an ordinary period, write it into the numerator, and write a number consisting of nines in an amount equal to the number of digits in the period into the denominator.
![]()
The mixed periodic decimal fraction is translated as follows:
- you need to form a number consisting of the number after the decimal point before the period and the first period;
- From the resulting number, subtract the number after the decimal point before the period. The result will be the numerator of the common fraction;
- in the denominator you need to enter a number consisting of a number of nines equal to the number of digits of the period, followed by zeros, the number of which is equal to the number of digits of the number after the decimal point before the 1st period.
![]()
![]()
Comparison of decimals
Decimal fractions are compared initially by their whole parts. The fraction whose whole part is larger is greater.
If the integer parts are the same, then compare the digits of the corresponding digits of the fractional part, starting from the first (from the tenths). The same principle applies here: the larger fraction is the one with more tenths; if the tenths digits are equal, the hundredths digits are compared, and so on.
Because the
![]() , since with equal whole parts and equal tenths in the fractional part, the 2nd fraction has a larger hundredths figure.
, since with equal whole parts and equal tenths in the fractional part, the 2nd fraction has a larger hundredths figure.
Adding and subtracting decimals
Decimals are added and subtracted in the same way as whole numbers by writing the corresponding digits below each other. To do this, you need to have decimal points below each other. Then the units (tens, etc.) of the integer part, as well as the tenths (hundredths, etc.) of the fractional part, will be in accordance. The missing digits of the fractional part are filled with zeros. Directly The process of addition and subtraction is carried out in the same way as for integers.
Multiplying Decimals
To multiply decimals, you need to write them one below the other, aligned with the last digit and not paying attention to the location of the decimal points. Then you need to multiply the numbers in the same way as when multiplying whole numbers. After receiving the result, you should recalculate the number of digits after the decimal point in both fractions and separate the total number of fractional digits in the resulting number with a comma. If there are not enough digits, they are replaced with zeros.

Multiplying and dividing decimals by 10n
These actions are simple and boil down to moving the decimal point. P When multiplying, the decimal point is moved to the right (the fraction is increased) by a number of digits equal to the number of zeros in 10n, where n is an arbitrary integer power. That is, a certain number of digits are transferred from the fractional part to the whole part. When dividing, accordingly, the comma is moved to the left (the number decreases), and some of the digits are transferred from the integer part to the fractional part. If there are not enough numbers to transfer, then the missing bits are filled with zeros.
Dividing a decimal and a whole number by a whole number and a decimal
Dividing a decimal by an integer is similar to dividing two integers. Additionally, you only need to take into account the position of the decimal point: when removing the digit of a place followed by a comma, you must place a comma after the current digit of the generated answer. Next you need to continue dividing until you get zero. If there are not enough signs in the dividend for complete division, zeros should be used as them.

Similarly, 2 integers are divided into a column if all the digits of the dividend are removed and the complete division is not yet completed. In this case, after removing the last digit of the dividend, a decimal point is placed in the resulting answer, and zeros are used as the removed digits. Those. the dividend here is essentially represented as a decimal fraction with a zero fractional part.

To divide a decimal fraction (or an integer) by a decimal number, you must multiply the dividend and divisor by the number 10 n, in which the number of zeros is equal to the number of digits after the decimal point in the divisor. In this way, you get rid of the decimal point in the fraction you want to divide by. Further, the division process coincides with that described above.
Graphical representation of decimal fractions
Decimal fractions are represented graphically using a coordinate line. To do this, individual segments are further divided into 10 equal parts, just as centimeters and millimeters are marked simultaneously on a ruler. This ensures that decimals are displayed accurately and can be compared objectively.
In order for the divisions on individual segments to be identical, you should carefully consider the length of the single segment itself. It should be such that the convenience of additional division can be ensured.
In this tutorial we will look at each of these operations separately.
Lesson contentAdding Decimals
As we know, a decimal fraction has an integer and a fractional part. When adding decimals, the whole and fractional parts are added separately.
For example, let's add the decimal fractions 3.2 and 5.3. It is more convenient to add decimal fractions in a column.
Let us first write these two fractions in a column, with the integer parts necessarily being under the integers, and the fractional parts under the fractional parts. At school this requirement is called "comma under comma".
Let's write the fractions in a column so that the comma is under the comma:
We begin to add the fractional parts: 2 + 3 = 5. We write the five in the fractional part of our answer:
Now we add up the whole parts: 3 + 5 = 8. We write an eight in the whole part of our answer:
Now we separate the whole part from the fractional part with a comma. To do this, we again follow the rule "comma under comma":
We received an answer of 8.5. So the expression 3.2 + 5.3 equals 8.5
In fact, not everything is as simple as it seems at first glance. There are also pitfalls here, which we will talk about now.
Places in decimals
Decimal fractions, like ordinary numbers, have their own digits. These are places of tenths, places of hundredths, places of thousandths. In this case, the digits begin after the decimal point.
The first digit after the decimal point is responsible for the tenths place, the second digit after the decimal point for the hundredths place, and the third digit after the decimal point for the thousandths place.
Places in decimal fractions contain some useful information. Specifically, they tell you how many tenths, hundredths, and thousandths there are in a decimal.
For example, consider the decimal fraction 0.345
The position where the three is located is called tenth place
The position where the four is located is called hundredths place
The position where the five is located is called thousandth place

Let's look at this drawing. We see that there is a three in the tenths place. This means that there are three tenths in the decimal fraction 0.345.
If we add the fractions, we get the original decimal fraction 0.345

It can be seen that at first we received the answer, but we converted it to a decimal fraction and got 0.345.
When adding decimal fractions, the same principles and rules are followed as when adding ordinary numbers. The addition of decimal fractions occurs in digits: tenths are added to tenths, hundredths to hundredths, thousandths to thousandths.
Therefore, when adding decimal fractions, you must follow the rule "comma under comma". The comma under the comma provides the very order in which tenths are added to tenths, hundredths to hundredths, thousandths to thousandths.
Example 1. Find the value of the expression 1.5 + 3.4
First of all, we add up the fractional parts 5 + 4 = 9. We write nine in the fractional part of our answer:
Now we add the integer parts 1 + 3 = 4. We write the four in the integer part of our answer:
Now we separate the whole part from the fractional part with a comma. To do this, we again follow the “comma under comma” rule:
We received an answer of 4.9. This means that the value of the expression 1.5 + 3.4 is 4.9
Example 2. Find the value of the expression: 3.51 + 1.22
We write this expression in a column, observing the “comma under comma” rule.
First of all, we add up the fractional part, namely the hundredths of 1+2=3. We write a triple in the hundredth part of our answer:
Now add the tenths 5+2=7. We write a seven in the tenth part of our answer:
Now we add the whole parts 3+1=4. We write the four in the whole part of our answer:
We separate the whole part from the fractional part with a comma, observing the “comma under comma” rule:
The answer we received was 4.73. This means the value of the expression 3.51 + 1.22 is equal to 4.73
3,51 + 1,22 = 4,73
As with regular numbers, when adding decimals, . In this case, one digit is written in the answer, and the rest are transferred to the next digit.
Example 3. Find the value of the expression 2.65 + 3.27
We write this expression in the column:
Add the hundredths parts 5+7=12. The number 12 will not fit into the hundredth part of our answer. Therefore, in the hundredth part we write the number 2, and move the unit to the next digit:
Now we add the tenths of 6+2=8 plus the unit that we got from the previous operation, we get 9. We write the number 9 in the tenth of our answer:
Now we add the whole parts 2+3=5. We write the number 5 in the integer part of our answer:
The answer we received was 5.92. This means the value of the expression 2.65 + 3.27 is equal to 5.92
2,65 + 3,27 = 5,92
Example 4. Find the value of the expression 9.5 + 2.8
We write this expression in the column
We add the fractional parts 5 + 8 = 13. The number 13 will not fit into the fractional part of our answer, so we first write down the number 3, and move the unit to the next digit, or rather, transfer it to the integer part:
Now we add the integer parts 9+2=11 plus the unit that we got from the previous operation, we get 12. We write the number 12 in the integer part of our answer:
Separate the whole part from the fractional part with a comma:
We received the answer 12.3. This means that the value of the expression 9.5 + 2.8 is 12.3
9,5 + 2,8 = 12,3
When adding decimals, the number of digits after the decimal point in both fractions must be the same. If there are not enough numbers, then these places in the fractional part are filled with zeros.
Example 5. Find the value of the expression: 12.725 + 1.7
Before writing this expression in a column, let’s make the number of digits after the decimal point in both fractions the same. The decimal fraction 12.725 has three digits after the decimal point, but the fraction 1.7 has only one. This means that in the fraction 1.7 you need to add two zeros at the end. Then we get the fraction 1.700. Now you can write this expression in a column and start calculating:

Add the thousandths parts 5+0=5. We write the number 5 in the thousandth part of our answer:

Add the hundredths parts 2+0=2. We write the number 2 in the hundredth part of our answer:

Add the tenths 7+7=14. The number 14 will not fit into a tenth of our answer. Therefore, we first write down the number 4, and move the unit to the next digit:

Now we add the integer parts 12+1=13 plus the unit that we got from the previous operation, we get 14. We write the number 14 in the integer part of our answer:

Separate the whole part from the fractional part with a comma:

We received a response of 14,425. This means the value of the expression 12.725+1.700 is 14.425
12,725+ 1,700 = 14,425
Subtracting Decimals
When subtracting decimal fractions, you must follow the same rules as when adding: “comma under the decimal point” and “equal number of digits after the decimal point.”
Example 1. Find the value of the expression 2.5 − 2.2
We write this expression in a column, observing the “comma under comma” rule:
We calculate the fractional part 5−2=3. We write the number 3 in the tenth part of our answer:
We calculate the integer part 2−2=0. We write zero in the integer part of our answer:
Separate the whole part from the fractional part with a comma:
We received an answer of 0.3. This means the value of the expression 2.5 − 2.2 is equal to 0.3
2,5 − 2,2 = 0,3
Example 2. Find the value of the expression 7.353 - 3.1
This expression has a different number of decimal places. The fraction 7.353 has three digits after the decimal point, but the fraction 3.1 has only one. This means that in the fraction 3.1 you need to add two zeros at the end to make the number of digits in both fractions the same. Then we get 3,100.
Now you can write this expression in a column and calculate it:

We received a response of 4,253. This means the value of the expression 7.353 − 3.1 is equal to 4.253
7,353 — 3,1 = 4,253
As with ordinary numbers, sometimes you will have to borrow one from an adjacent digit if subtraction becomes impossible.
Example 3. Find the value of the expression 3.46 − 2.39
Subtract hundredths of 6−9. You cannot subtract the number 9 from the number 6. Therefore, you need to borrow one from the adjacent digit. By borrowing one from the adjacent digit, the number 6 turns into the number 16. Now you can calculate the hundredths of 16−9=7. We write a seven in the hundredth part of our answer:
Now we subtract tenths. Since we took one unit in the tenths place, the figure that was located there decreased by one unit. In other words, in the tenths place there is now not the number 4, but the number 3. Let's calculate the tenths of 3−3=0. We write zero in the tenth part of our answer:
Now we subtract the whole parts 3−2=1. We write one in the integer part of our answer:
Separate the whole part from the fractional part with a comma:
We received an answer of 1.07. This means the value of the expression 3.46−2.39 is equal to 1.07
3,46−2,39=1,07
Example 4. Find the value of the expression 3−1.2
This example subtracts a decimal from a whole number. Let's write this expression in a column so that the whole part of the decimal fraction 1.23 is under the number 3
Now let's make the number of digits after the decimal point the same. To do this, after the number 3 we put a comma and add one zero:
Now we subtract tenths: 0−2. You cannot subtract the number 2 from zero. Therefore, you need to borrow one from the adjacent digit. Having borrowed one from the neighboring digit, 0 turns into the number 10. Now you can calculate the tenths of 10−2=8. We write an eight in the tenth part of our answer:
Now we subtract the whole parts. Previously, the number 3 was located in the whole, but we took one unit from it. As a result, it turned into the number 2. Therefore, from 2 we subtract 1. 2−1=1. We write one in the integer part of our answer:
Separate the whole part from the fractional part with a comma:
The answer we received was 1.8. This means the value of the expression 3−1.2 is 1.8
Multiplying Decimals
Multiplying decimals is simple and even fun. To multiply decimals, you multiply them like regular numbers, ignoring the commas.
Having received the answer, you need to separate the whole part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in both fractions, then count the same number of digits from the right in the answer and put a comma.
Example 1. Find the value of the expression 2.5 × 1.5
Let's multiply these decimal fractions like ordinary numbers, ignoring the commas. To ignore the commas, you can temporarily imagine that they are absent altogether:

We got 375. In this number, you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fractions 2.5 and 1.5. The first fraction has one digit after the decimal point, and the second fraction also has one. Total two numbers.
We return to the number 375 and begin to move from right to left. We need to count two digits to the right and put a comma:

We received an answer of 3.75. So the value of the expression 2.5 × 1.5 is 3.75
2.5 × 1.5 = 3.75
Example 2. Find the value of the expression 12.85 × 2.7
Let's multiply these decimal fractions, ignoring the commas:

We got 34695. In this number you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fractions 12.85 and 2.7. The fraction 12.85 has two digits after the decimal point, and the fraction 2.7 has one digit - a total of three digits.
We return to the number 34695 and begin to move from right to left. We need to count three digits from the right and put a comma:

We received a response of 34,695. So the value of the expression 12.85 × 2.7 is 34.695
12.85 × 2.7 = 34.695
Multiplying a decimal by a regular number
Sometimes situations arise when you need to multiply a decimal fraction by a regular number.
To multiply a decimal and a number, you multiply them without paying attention to the comma in the decimal. Having received the answer, you need to separate the whole part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the decimal fraction, then count the same number of digits from the right in the answer and put a comma.
For example, multiply 2.54 by 2
Multiply the decimal fraction 2.54 by the usual number 2, ignoring the comma:

We got the number 508. In this number you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fraction 2.54. The fraction 2.54 has two digits after the decimal point.
We return to number 508 and begin to move from right to left. We need to count two digits to the right and put a comma:

We received an answer of 5.08. So the value of the expression 2.54 × 2 is 5.08
2.54 × 2 = 5.08
Multiplying decimals by 10, 100, 1000
Multiplying decimals by 10, 100, or 1000 is done in the same way as multiplying decimals by regular numbers. You need to perform the multiplication, not paying attention to the comma in the decimal fraction, then in the answer, separate the whole part from the fractional part, counting from the right the same number of digits as there were digits after the decimal point.
For example, multiply 2.88 by 10
Multiply the decimal fraction 2.88 by 10, ignoring the comma in the decimal fraction:

We got 2880. In this number you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fraction 2.88. We see that the fraction 2.88 has two digits after the decimal point.
We return to the number 2880 and begin to move from right to left. We need to count two digits to the right and put a comma:

We received an answer of 28.80. Let's drop the last zero and get 28.8. This means that the value of the expression 2.88×10 is 28.8
2.88 × 10 = 28.8
There is a second way to multiply decimal fractions by 10, 100, 1000. This method is much simpler and more convenient. It consists in moving the decimal point to the right by as many digits as there are zeros in the factor.
For example, let's solve the previous example 2.88×10 this way. Without giving any calculations, we immediately look at the factor 10. We are interested in how many zeros there are in it. We see that there is one zero in it. Now in the fraction 2.88 we move the decimal point to the right one digit, we get 28.8.
2.88 × 10 = 28.8
Let's try to multiply 2.88 by 100. We immediately look at the factor 100. We are interested in how many zeros there are in it. We see that there are two zeros in it. Now in the fraction 2.88 we move the decimal point to the right two digits, we get 288
2.88 × 100 = 288
Let's try to multiply 2.88 by 1000. We immediately look at the factor 1000. We are interested in how many zeros there are in it. We see that there are three zeros in it. Now in the fraction 2.88 we move the decimal point to the right by three digits. There is no third digit there, so we add another zero. As a result, we get 2880.
2.88 × 1000 = 2880
Multiplying decimals by 0.1 0.01 and 0.001
Multiplying decimals by 0.1, 0.01, and 0.001 works in the same way as multiplying a decimal by a decimal. It is necessary to multiply the fractions like ordinary numbers, and put a comma in the answer, counting as many digits to the right as there are digits after the decimal point in both fractions.
For example, multiply 3.25 by 0.1
We multiply these fractions like ordinary numbers, ignoring the commas:

We got 325. In this number you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fractions 3.25 and 0.1. The fraction 3.25 has two digits after the decimal point, and the fraction 0.1 has one digit. Total three numbers.
We return to the number 325 and begin to move from right to left. We need to count three digits from the right and put a comma. After counting down three digits, we find that the numbers have run out. In this case, you need to add one zero and add a comma:

We received an answer of 0.325. This means that the value of the expression 3.25 × 0.1 is 0.325
3.25 × 0.1 = 0.325
There is a second way to multiply decimals by 0.1, 0.01 and 0.001. This method is much simpler and more convenient. It consists in moving the decimal point to the left by as many digits as there are zeros in the factor.
For example, let's solve the previous example 3.25 × 0.1 this way. Without giving any calculations, we immediately look at the multiplier of 0.1. We are interested in how many zeros there are in it. We see that there is one zero in it. Now in the fraction 3.25 we move the decimal point to the left by one digit. By moving the comma one digit to the left, we see that there are no more digits before the three. In this case, add one zero and put a comma. The result is 0.325
3.25 × 0.1 = 0.325
Let's try multiplying 3.25 by 0.01. We immediately look at the multiplier of 0.01. We are interested in how many zeros there are in it. We see that there are two zeros in it. Now in the fraction 3.25 we move the decimal point to the left two digits, we get 0.0325
3.25 × 0.01 = 0.0325
Let's try multiplying 3.25 by 0.001. We immediately look at the multiplier of 0.001. We are interested in how many zeros there are in it. We see that there are three zeros in it. Now in the fraction 3.25 we move the decimal point to the left by three digits, we get 0.00325
3.25 × 0.001 = 0.00325
Do not confuse multiplying decimal fractions by 0.1, 0.001 and 0.001 with multiplying by 10, 100, 1000. Common mistake most people.
When multiplying by 10, 100, 1000, the decimal point is moved to the right by the same number of digits as there are zeros in the multiplier.
And when multiplying by 0.1, 0.01 and 0.001, the decimal point is moved to the left by the same number of digits as there are zeros in the multiplier.
If at first it is difficult to remember, you can use the first method, in which multiplication is performed as with ordinary numbers. In the answer, you will need to separate the whole part from the fractional part, counting the same number of digits on the right as there are digits after the decimal point in both fractions.
Dividing a smaller number by a larger number. Advanced level.
In one of the previous lessons, we said that when dividing a smaller number by a larger number, a fraction is obtained, the numerator of which is the dividend, and the denominator is the divisor.
For example, to divide one apple between two, you need to write 1 (one apple) in the numerator, and write 2 (two friends) in the denominator. As a result, we get the fraction . This means each friend will get an apple. In other words, half an apple. The fraction is the answer to the problem “how to divide one apple into two”

It turns out that you can solve this problem further if you divide 1 by 2. After all, the fractional line in any fraction means division, and therefore this division is allowed in the fraction. But how? We are accustomed to the fact that the dividend is always greater than the divisor. But here, on the contrary, the dividend is less than the divisor.
Everything will become clear if we remember that a fraction means crushing, division, division. This means that the unit can be split into as many parts as desired, and not just into two parts.
When you divide a smaller number by a larger number, you get a decimal fraction in which the integer part is 0 (zero). The fractional part can be anything.
So, let's divide 1 by 2. Let's solve this example with a corner:
One cannot be completely divided into two. If you ask a question “how many twos are there in one” , then the answer will be 0. Therefore, in the quotient we write 0 and put a comma:
Now, as usual, we multiply the quotient by the divisor to get the remainder:
The moment has come when the unit can be split into two parts. To do this, add another zero to the right of the resulting one:
We got 10. Divide 10 by 2, we get 5. We write the five in the fractional part of our answer:
Now we take out the last remainder to complete the calculation. Multiply 5 by 2 to get 10
We received an answer of 0.5. So the fraction is 0.5
Half an apple can also be written using the decimal fraction 0.5. If we add these two halves (0.5 and 0.5), we again get the original one whole apple: 

This point can also be understood if you imagine how 1 cm is divided into two parts. If you divide 1 centimeter into 2 parts, you get 0.5 cm

Example 2. Find the value of the expression 4:5
How many fives are there in a four? Not at all. We write 0 in the quotient and put a comma:
We multiply 0 by 5, we get 0. We write a zero under the four. Immediately subtract this zero from the dividend:
Now let's start splitting (dividing) the four into 5 parts. To do this, add a zero to the right of 4 and divide 40 by 5, we get 8. We write eight in the quotient.

We complete the example by multiplying 8 by 5 to get 40:

We received an answer of 0.8. This means the value of the expression 4:5 is 0.8
Example 3. Find the value of expression 5: 125
How many numbers are 125 in five? Not at all. We write 0 in the quotient and put a comma:

We multiply 0 by 5, we get 0. We write 0 under the five. Immediately subtract 0 from five

Now let's start splitting (dividing) the five into 125 parts. To do this, we write a zero to the right of this five:

Divide 50 by 125. How many numbers are 125 in the number 50? Not at all. So in the quotient we write 0 again

Multiply 0 by 125, we get 0. Write this zero under 50. Immediately subtract 0 from 50
Now divide the number 50 into 125 parts. To do this, we write another zero to the right of 50:
Divide 500 by 125. How many numbers are 125 in the number 500? There are four numbers 125 in the number 500. Write the four in the quotient:

We complete the example by multiplying 4 by 125 to get 500

We received an answer of 0.04. This means the value of expression 5: 125 is 0.04
Dividing numbers without a remainder
So, let’s put a comma after the unit in the quotient, thereby indicating that the division of integer parts is over and we are proceeding to the fractional part:
Let's add zero to the remainder 4
Now divide 40 by 5, we get 8. We write eight in the quotient:
40−40=0. We got 0 left. This means that the division is completely completed. Dividing 9 by 5 gives the decimal fraction 1.8:
9: 5 = 1,8
Example 2. Divide 84 by 5 without a remainder
First, divide 84 by 5 as usual with a remainder:

We got 16 in private and 4 more left. Now let's divide this remainder by 5. Put a comma in the quotient, and add 0 to the remainder 4

Now we divide 40 by 5, we get 8. We write the eight in the quotient after the decimal point:

and complete the example by checking whether there is still a remainder:

Dividing a decimal by a regular number
A decimal fraction, as we know, consists of an integer and a fractional part. When dividing a decimal fraction by a regular number, you first need to:
- divide the whole part of the decimal fraction by this number;
- after the whole part is divided, you need to immediately put a comma in the quotient and continue the calculation, as in normal division.
For example, divide 4.8 by 2
Let's write this example in a corner:

Now let's divide the whole part by 2. Four divided by two equals two. We write two in the quotient and immediately put a comma:
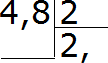
Now we multiply the quotient by the divisor and see if there is a remainder from the division:

4−4=0. The remainder is zero. We do not write down zero yet, since the solution is not completed. Next, we continue to calculate as in ordinary division. Take down 8 and divide it by 2

8: 2 = 4. We write the four in the quotient and immediately multiply it by the divisor:

We received an answer of 2.4. The value of the expression 4.8:2 is 2.4
Example 2. Find the value of the expression 8.43: 3

Divide 8 by 3, we get 2. Immediately put a comma after the 2:

Now we multiply the quotient by the divisor 2 × 3 = 6. We write the six under the eight and find the remainder:
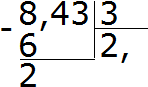

Divide 24 by 3, we get 8. We write eight in the quotient. Immediately multiply it by the divisor to find the remainder of the division:

24−24=0. The remainder is zero. We don’t write down zero yet. We take away the last three from the dividend and divide by 3, we get 1. Immediately multiply 1 by 3 to complete this example:

The answer we received was 2.81. This means the value of the expression 8.43: 3 is 2.81
Dividing a decimal by a decimal
To divide a decimal fraction by a decimal fraction, you need to move the decimal point in the dividend and divisor to the right by the same number of digits as there are after the decimal point in the divisor, and then divide by the usual number.
For example, divide 5.95 by 1.7
Let's write this expression with a corner

Now in the dividend and in the divisor we move the decimal point to the right by the same number of digits as there are after the decimal point in the divisor. The divisor has one digit after the decimal point. This means that in the dividend and divisor we must move the decimal point to the right by one digit. We transfer:

After moving the decimal point to the right one digit, the decimal fraction 5.95 became the fraction 59.5. And the decimal fraction 1.7, after moving the decimal point to the right by one digit, turned into the usual number 17. And we already know how to divide a decimal fraction by a regular number. Further calculation is not difficult:

The comma is moved to the right to make division easier. This is allowed because when multiplying or dividing the dividend and the divisor by the same number, the quotient does not change. What does it mean?
This is one of interesting features division. It is called the quotient property. Consider expression 9: 3 = 3. If in this expression the dividend and the divisor are multiplied or divided by the same number, then the quotient 3 will not change.
Let's multiply the dividend and divisor by 2 and see what comes out of it:
(9 × 2) : (3 × 2) = 18: 6 = 3
As can be seen from the example, the quotient has not changed.
The same thing happens when we move the comma in the dividend and in the divisor. In the previous example, where we divided 5.91 by 1.7, we moved the comma in the dividend and divisor one digit to the right. After moving the decimal point, the fraction 5.91 was transformed into the fraction 59.1 and the fraction 1.7 was transformed into the usual number 17.
In fact, inside this process there was a multiplication by 10. This is what it looked like:
5.91 × 10 = 59.1
Therefore, the number of digits after the decimal point in the divisor determines what the dividend and divisor will be multiplied by. In other words, the number of digits after the decimal point in the divisor will determine how many digits in the dividend and in the divisor the decimal point will be moved to the right.
Dividing a decimal by 10, 100, 1000
Dividing a decimal by 10, 100, or 1000 is done in the same way as . For example, divide 2.1 by 10. Solve this example using a corner:

But there is a second way. It's lighter. The essence of this method is that the comma in the dividend is moved to the left by as many digits as there are zeros in the divisor.
Let's solve the previous example this way. 2.1: 10. We look at the divisor. We are interested in how many zeros there are in it. We see that there is one zero. This means that in the dividend of 2.1 you need to move the decimal point to the left by one digit. We move the comma to the left one digit and see that there are no more digits left. In this case, add another zero before the number. As a result we get 0.21
Let's try to divide 2.1 by 100. There are two zeros in 100. This means that in the dividend 2.1 we need to move the comma to the left by two digits:
2,1: 100 = 0,021
Let's try to divide 2.1 by 1000. There are three zeros in 1000. This means that in the dividend 2.1 you need to move the comma to the left by three digits:
2,1: 1000 = 0,0021
Dividing a decimal by 0.1, 0.01 and 0.001
Dividing a decimal fraction by 0.1, 0.01, and 0.001 is done in the same way as . In the dividend and in the divisor, you need to move the decimal point to the right by as many digits as there are after the decimal point in the divisor.
For example, let's divide 6.3 by 0.1. First of all, let’s move the commas in the dividend and divisor to the right by the same number of digits as there are after the decimal point in the divisor. The divisor has one digit after the decimal point. This means we move the commas in the dividend and divisor to the right by one digit.
After moving the decimal point to the right one digit, the decimal fraction 6.3 becomes the usual number 63, and the decimal fraction 0.1 after moving the decimal point to the right one digit turns into one. And dividing 63 by 1 is very simple:
This means the value of the expression 6.3: 0.1 is 63
But there is a second way. It's lighter. The essence of this method is that the comma in the dividend is moved to the right by as many digits as there are zeros in the divisor.
Let's solve the previous example this way. 6.3: 0.1. Let's look at the divisor. We are interested in how many zeros there are in it. We see that there is one zero. This means that in the dividend of 6.3 you need to move the decimal point to the right by one digit. Move the comma to the right one digit and get 63
Let's try to divide 6.3 by 0.01. The divisor of 0.01 has two zeros. This means that in the dividend 6.3 we need to move the decimal point to the right by two digits. But in the dividend there is only one digit after the decimal point. In this case, you need to add another zero at the end. As a result we get 630
Let's try to divide 6.3 by 0.001. The divisor of 0.001 has three zeros. This means that in the dividend 6.3 we need to move the decimal point to the right by three digits:
6,3: 0,001 = 6300
Tasks for independent solution
Did you like the lesson?
Join our new group VKontakte and start receiving notifications about new lessons
Already in primary school students encounter fractions. And then they appear in every topic. You cannot forget actions with these numbers. Therefore, you need to know all the information about ordinary and decimal fractions. These concepts are not complicated, the main thing is to understand everything in order.
Why are fractions needed?
The world around us consists of entire objects. Therefore, there is no need for shares. But everyday life constantly pushes people to work with parts of objects and things.
For example, chocolate consists of several pieces. Consider a situation where his tile is formed by twelve rectangles. If you divide it into two, you get 6 parts. It can easily be divided into three. But it will not be possible to give five people a whole number of chocolate slices.
By the way, these slices are already fractions. And their further division leads to the appearance of more complex numbers.
What is a "fraction"?
This is a number made up of parts of a unit. Outwardly, it looks like two numbers separated by a horizontal or slash. This feature is called fractional. The number written at the top (left) is called the numerator. What is at the bottom (right) is the denominator.
Essentially, the slash turns out to be a division sign. That is, the numerator can be called the dividend, and the denominator can be called the divisor.
What fractions are there?
In mathematics there are only two types: ordinary and decimal fractions. Schoolchildren first meet in primary school, calling them simply "fractions". The latter will be learned in 5th grade. That's when these names appear.
Common fractions are all those that are written as two numbers separated by a line. For example, 4/7. A decimal is a number in which the fractional part has a positional notation and is separated from the whole number by a comma. For example, 4.7. Students need to clearly understand that the two examples given are completely different numbers.
Every simple fraction can be written as a decimal. This statement is almost always true in reverse. There are rules that allow you to write a decimal fraction as a common fraction.

What subtypes do these types of fractions have?
It's better to start in chronological order, as they are being studied. Common fractions come first. Among them, 5 subspecies can be distinguished.
Correct. Its numerator is always less than its denominator.
Wrong. Its numerator is greater than or equal to its denominator.
Reducible/irreducible. It may turn out to be either right or wrong. Another important thing is whether the numerator and denominator have common factors. If there are, then it is necessary to divide both parts of the fraction by them, that is, reduce it.
Mixed. An integer is assigned to its usual regular (irregular) fractional part. Moreover, it is always on the left.
Composite. It is formed from two fractions divided by each other. That is, it contains three fractional lines at once.
Decimal fractions have only two subtypes:
finite, that is, one whose fractional part is limited (has an end);
infinite - a number whose digits after the decimal point do not end (they can be written endlessly).

How to convert a decimal fraction to a common fraction?
If this is a finite number, then an association is applied based on the rule - as I hear, so I write. That is, you need to read it correctly and write it down, but without a comma, but with a fractional bar.
As a hint about the required denominator, you need to remember that it is always one and several zeros. You need to write as many of the latter as there are digits in the fractional part of the number in question.
How to convert decimal fractions into ordinary fractions if their integer part is missing, that is, equal to zero? For example, 0.9 or 0.05. After applying the specified rule, it turns out that you need to write zero integers. But it is not indicated. All that remains is to write down the fractional parts. The first number will have a denominator of 10, the second will have a denominator of 100. That is, the given examples will have the following numbers as answers: 9/10, 5/100. Moreover, it turns out that the latter can be reduced by 5. Therefore, the result for it needs to be written as 1/20.
How can you convert a decimal fraction into an ordinary fraction if its integer part is different from zero? For example, 5.23 or 13.00108. In both examples, the whole part is read and its value is written. In the first case it is 5, in the second it is 13. Then you need to move on to the fractional part. The same operation is supposed to be carried out with them. The first number appears 23/100, the second - 108/100000. The second value needs to be reduced again. The answer looks like this mixed fractions: 5 23/100 and 13 27/25000.

How to convert an infinite decimal fraction to an ordinary fraction?
If it is non-periodic, then such an operation will not be possible. This fact is due to the fact that each decimal fraction is always converted to either a finite or a periodic fraction.
The only thing you can do with such a fraction is round it. But then the decimal will be approximately equal to that infinite. It can already be turned into an ordinary one. But reverse process: converting to decimal will never give the initial value. That is, infinite non-periodic fractions are not converted into ordinary fractions. This needs to be remembered.
How to write an infinite periodic fraction as an ordinary fraction?
In these numbers, there are always one or more digits after the decimal point that are repeated. They are called a period. For example, 0.3(3). Here "3" is in the period. They are classified as rational because they can be converted into ordinary fractions.
Those who have encountered periodic fractions know that they can be pure or mixed. In the first case, the period starts immediately from the comma. In the second, the fractional part begins with some numbers, and then the repetition begins.
The rule by which you need to write an infinite decimal as a common fraction will be different for the two types of numbers indicated. It is quite easy to write pure periodic fractions as ordinary fractions. As with finite ones, they need to be converted: write down the period in the numerator, and the denominator will be the number 9, repeated as many times as the number of digits the period contains.
For example, 0,(5). The number does not have an integer part, so you need to immediately start with the fractional part. Write 5 as the numerator and 9 as the denominator. That is, the answer will be the fraction 5/9.
The rule on how to write an ordinary decimal periodic fraction that is mixed.
Look at the length of the period. That's how many 9s the denominator will have.
Write down the denominator: first nines, then zeros.
To determine the numerator, you need to write down the difference of two numbers. All numbers after the decimal point will be minified, along with the period. Deductible - it is without a period.
For example, 0.5(8) - write the periodic decimal fraction as a common fraction. The fractional part before the period contains one digit. So there will be one zero. There is also only one number in the period - 8. That is, there is only one nine. That is, you need to write 90 in the denominator.
To determine the numerator, you need to subtract 5 from 58. It turns out 53. For example, you would have to write the answer as 53/90.

How are fractions converted to decimals?
The simplest option is a number whose denominator is the number 10, 100, etc. Then the denominator is simply discarded, and a comma is placed between the fractional and integer parts.
There are situations when the denominator easily turns into 10, 100, etc. For example, the numbers 5, 20, 25. It is enough to multiply them by 2, 5 and 4, respectively. You just need to multiply not only the denominator, but also the numerator by the same number.
For all other cases, a simple rule is useful: divide the numerator by the denominator. In this case, you may get two possible answers: a finite or a periodic decimal fraction.
Operations with ordinary fractions
Addition and subtraction
Students become acquainted with them earlier than others. And first for fractions same denominators, and then different. General rules can be reduced to such a plan.
Find the least common multiple of the denominators.
Write additional factors for all ordinary fractions.
Multiply the numerators and denominators by the factors specified for them.
Add (subtract) the numerators of the fractions and leave the common denominator unchanged.
If the numerator of the minuend is less than the subtrahend, then we need to find out whether we have a mixed number or a proper fraction.
In the first case, you need to borrow one from the whole part. Add the denominator to the numerator of the fraction. And then do the subtraction.
In the second, it is necessary to apply the rule of subtracting a larger number from a smaller number. That is, from the module of the subtrahend, subtract the module of the minuend, and in response put a “-” sign.
Look carefully at the result of addition (subtraction). If you get an improper fraction, then you need to select the whole part. That is, divide the numerator by the denominator.
Multiplication and division
To perform them, fractions do not need to be reduced to a common denominator. This makes it easier to perform actions. But they still require you to follow the rules.
When multiplying fractions, you need to look at the numbers in the numerators and denominators. If any numerator and denominator have a common factor, then they can be reduced.
Multiply the numerators.
Multiply the denominators.
If the result is a reducible fraction, then it must be simplified again.
When dividing, you must first replace division with multiplication, and the divisor (second fraction) with the reciprocal fraction (swap the numerator and denominator).
Then proceed as with multiplication (starting from point 1).
In tasks where you need to multiply (divide) by a whole number, the latter should be written as an improper fraction. That is, with a denominator of 1. Then act as described above.

Operations with decimals
Addition and subtraction
Of course, you can always convert a decimal into a fraction. And act according to the plan already described. But sometimes it is more convenient to act without this translation. Then the rules for their addition and subtraction will be exactly the same.
Equalize the number of digits in the fractional part of the number, that is, after the decimal point. Add the missing number of zeros to it.
Write the fractions so that the comma is below the comma.
Add (subtract) like natural numbers.
Remove the comma.
Multiplication and division
It is important that you do not need to add zeros here. Fractions should be left as they are given in the example. And then go according to plan.
To multiply, you need to write the fractions one below the other, ignoring the commas.
Multiply like natural numbers.
Place a comma in the answer, counting from the right end of the answer as many digits as there are in fractional parts both multipliers.
To divide you must first convert the divisor: make it natural number. That is, multiply it by 10, 100, etc., depending on how many digits are in the fractional part of the divisor.
Multiply the dividend by the same number.
Divide a decimal fraction by a natural number.
Place a comma in your answer at the moment when the division of the whole part ends.

What if one example contains both types of fractions?
Yes, in mathematics there are often examples in which you need to perform operations on ordinary and decimal fractions. In such tasks there are two possible solutions. You need to objectively weigh the numbers and choose the optimal one.
First way: represent ordinary decimals
It is suitable if division or translation results in finite fractions. If at least one number gives a periodic part, then this technique is prohibited. Therefore, even if you don’t like working with ordinary fractions, you will have to count them.
Second way: write decimal fractions as ordinary
This technique turns out to be convenient if the part after the decimal point contains 1-2 digits. If there are more of them, you may end up with a very large common fraction and decimal notation will make the task faster and easier to calculate. Therefore, you always need to soberly evaluate the task and choose the simplest solution method.
For example.$\frac(3)(10), 4 \frac(7)(100), \frac(11)(10000)$
Such fractions are usually written without a denominator, and the meaning of each digit depends on the place in which it stands. For such fractions, the integer part is separated by a comma, and after the decimal point there must be as many digits as there are zeros in the denominator of the common fraction. The fractional digits are called decimals.
For example.$\frac(21)(100)=0.21 ; 3 \frac(21)(100)=$3.21
The first decimal place after the decimal point corresponds to tenths, the second to hundredths, the third to thousandths, etc.
If the number of zeros in the denominator of a decimal fraction is greater than the number of digits in the numerator of the same fraction, then the required number of zeros is added after the decimal point before the numerator digits.

Since there are four zeros in the denominator, and two digits in the numerator, in the decimal notation of the fraction we add $4-2=2$ zeros before the numerator.
The main property of a decimal fraction
Property
If you add several zeros to the decimal fraction on the right, the value of the decimal fraction will not change.
For example.$12,034=12,0340=12,03400=12,034000=\ldots$
Comment
Thus, zeros at the end of the decimal are not taken into account, so when doing various actions these zeros can be crossed out/discarded.
Comparison of decimals
To compare two decimal fractions (to find out which of two decimal fractions is larger), you need to compare their whole parts, then tenths, hundredths, etc. If the whole part of one of the fractions is greater than the whole part of another fraction, then the first fraction is considered larger. In the case of equality of whole parts, the fraction with more tenths is greater, etc.
Example
Exercise. Compare fractions $2,432$ ; $2.41$ and $1,234$
Solution. The fraction $1.234$ is the smallest fraction because its integer part is 1, and $1
Let us now compare the size of the fractions $2.432$ and $1.234$. Their whole parts are equal to each other and equal to 2. Let's compare the tenths: $4=4$. Compare hundredths: $3>1$. Thus, $2.432>$2.41.
To rational number m/n is written as a decimal fraction; you need to divide the numerator by the denominator. In this case, the quotient is written as a finite or infinite decimal fraction.
Write this number as a decimal fraction.
Solution. Divide the numerator of each fraction into a column by its denominator: A) divide 6 by 25; b) divide 2 by 3; V) divide 1 by 2, and then add the resulting fraction to one - the integer part of this mixed number.

Irreducible ordinary fractions whose denominators do not contain prime factors other than 2 And 5 , are written as a final decimal fraction.
IN example 1 when A) denominator 25=5·5; when V) the denominator is 2, so we get the final decimals 0.24 and 1.5. When b) the denominator is 3, so the result cannot be written as a finite decimal.
Is it possible, without long division, to convert into a decimal fraction such an ordinary fraction, the denominator of which does not contain other divisors other than 2 and 5? Let's figure it out! What fraction is called a decimal and is written without a fraction bar? Answer: fraction with denominator 10; 100; 1000, etc. And each of these numbers is a product equal number of twos and fives. In fact: 10=2 ·5 ; 100=2 ·5 ·2 ·5 ; 1000=2 ·5 ·2 ·5 ·2 ·5 etc.
Consequently, the denominator of an irreducible ordinary fraction will need to be represented as the product of “twos” and “fives”, and then multiplied by 2 and (or) 5 so that the “twos” and “fives” become equal. Then the denominator of the fraction will be equal to 10 or 100 or 1000, etc. To ensure that the value of the fraction does not change, we multiply the numerator of the fraction by the same number by which we multiplied the denominator.
Express the following common fractions as decimals:
![]()
Solution. Each of these fractions is irreducible. Let's factor the denominator of each fraction into prime factors.
20=2·2·5. Conclusion: one “A” is missing.
8=2·2·2. Conclusion: three “A”s are missing.
25=5·5. Conclusion: two “twos” are missing.

Comment. In practice, they often do not use factorization of the denominator, but simply ask the question: by how much should the denominator be multiplied so that the result is one with zeros (10 or 100 or 1000, etc.). And then the numerator is multiplied by the same number.
So, in case A)(example 2) from the number 20 you can get 100 by multiplying by 5, therefore, you need to multiply the numerator and denominator by 5.
When b)(example 2) from the number 8 the number 100 will not be obtained, but the number 1000 will be obtained by multiplying by 125. Both the numerator (3) and the denominator (8) of the fraction are multiplied by 125.
When V)(example 2) from 25 you get 100 if you multiply by 4. This means that the numerator 8 must be multiplied by 4.
An infinite decimal fraction in which one or more digits invariably repeat in the same sequence is called periodic as a decimal. The set of repeating digits is called the period of this fraction. For brevity, the period of a fraction is written once, enclosed in parentheses.
When b)(example 1) there is only one repeating digit and is equal to 6. Therefore, our result 0.66... will be written like this: 0,(6) . They read: zero point, six in period.
If there are one or more non-repeating digits between the decimal point and the first period, then such a periodic fraction is called a mixed periodic fraction.
An irreducible common fraction whose denominator is together with others multiplier contains multiplier 2 or 5 , becomes mixed periodic fraction.
Write numbers as decimals.

 Entrance
Entrance