home / Success stories/ Derivative. Continuity of a function having a derivative Properties of functions continuous on an interval

Derivative. Continuity of a function having a derivative Properties of functions continuous on an interval

The function y=f(x) is called differentiable at some point x 0 if it has a certain derivative at this point, i.e. if the limit of the relationship exists and is finite.

If a function is differentiable at each point of a certain segment [a; b] or interval (a; b), then we say that it is differentiable on the interval [a; b] or, respectively, in the interval (a; b).

The following theorem is valid, establishing the connection between differentiable and continuous functions.

Theorem. If the function y=f(x) is differentiable at some point x 0, then it is continuous at this point.

Thus, from the differentiability of a function, its continuity follows.

Proof. If, then

where b is an infinitesimal quantity, i.e. a quantity tending to zero when Dx>0. But then

Dy=f "(x 0) Dx+bDx=> Dy>0 at Dx>0, i.e. f(x) - f(x 0)>0 at x>x 0,

and this means that the function f(x) is continuous at the point x 0 . Q.E.D.

Thus, the function cannot have a derivative at discontinuity points. The converse is not true: there are continuous functions that are not differentiable at some points (that is, do not have a derivative at these points).

Let's look at points a, b, c in the figure.

At point a for Dx>0, the ratio has no limit (since one-sided limits are different for Dx>0-0 and Dx>0+0). At point A of the graph there is no specific tangent, but there are two different one-way tangents with slopes of 1 and 2. This type of point is called corner point.

At point b for Dx>0, the ratio is of constant sign and infinitely large. The function has infinite derivative. At this point the graph has a vertical tangent. Point type - “inflection point” with a vertical tangent.

At point c, the one-sided derivatives are infinitely large quantities of different signs. At this point the graph has two merged vertical tangents. Type - "return point" with a vertical tangent - a special case of a corner point.

1. Consider the function y=|x|. This function is continuous at the point

Let us show that it has no derivative at this point.

f(0+Dx) = f(Dx) = |Dx|. Therefore, Дy = f(Дx) - f(0) = |Дx|

But then at Dx< 0 (т.е. при Дx стремящемся к 0 слева)

And when Dx > 0

Thus, the ratio for Dx> 0 on the right and left has different limits, which means that the ratio has no limit, i.e. derivative of the function y=|x| does not exist at point x= 0. Geometrically, this means that at the point x = 0 this “curve” does not have a specific tangent (at this point there are two of them).

2. The function is defined and continuous on the entire number line. Let's find out whether this function has a derivative at x= 0.

Consequently, the function under consideration is not differentiable at the point x= 0. The tangent to the curve at this point forms an angle p/2 with the abscissa axis, i.e. coincides with the Oy axis.

Function y = f(x) called differentiable at some point x 0 if it has a certain derivative at this point, i.e. if the limit of the relationship exists and is finite.

If a function is differentiable at each point of a certain segment [ A; b] or interval ( A; b), then they say that she differentiable on the segment [ A; b] or, respectively, in the interval ( A; b).

The following theorem is valid, establishing the connection between differentiable and continuous functions.

Theorem. If the function y = f(x) differentiable at some point x 0, then it is continuous at this point.

Thus, from the differentiability of a function, its continuity follows.

Proof . If , then

where α is an infinitesimal quantity, i.e. a quantity tending to zero as Δ x→0. But then

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 at Δ x→0, i.e. f(x) - f(x 0)→0 at x→x 0 , which means that the function f(x) continuous at a point x 0 . Q.E.D.

Consider the points in the figure a, b, c.

At the point a at Δ x→0 the ratio has no limit (since the one-sided limits are different for Δ x→0-0 and Δ x→0+0). At the point A graph there is no defined tangent, but there are two different one-way tangents with slopes To 1 and To 2. This type of point is called corner point.

At the point b at Δ x The →0 ratio is a constant sign infinitely large quantity. The function has infinite derivative. At this point the graph has a vertical tangent. Point type - “inflection point” with a vertical tangent.

At the point c one-sided derivatives are infinitely large quantities of different signs. At this point the graph has two merged vertical tangents. Type - "return point" with a vertical tangent - a special case of a corner point.

Examples.

1. Consider the function y=|x|. This function is continuous at the point x= 0, because .

Let us show that it has no derivative at this point.

f(0+Δ x) = f(Δ x) = |Δ x|. Therefore, Δ y = f(Δ x) - f(0) = |Δ x|

But then for Δ x< 0 (т.е. при Δx tending to 0 on the left)

And at Δ x > 0

Thus, the ratio at Δ x→ 0 on the right and left has different limits, which means that the ratio has no limit, i.e. derivative of a function y=|x| at the point x= 0 does not exist. Geometrically this means that at the point x= 0 this “curve” does not have a defined tangent (at this point there are two).

2. The function is defined and continuous on the entire number line. Let's find out whether this function has a derivative at x= 0.

Derivatives of elementary functions.

1.
y = xn. If n is a positive integer, then, using Newton’s binomial formula:

(a + b) n = a n+ n·a n-1 b + 1/2?n(n - 1)a n-2 ? b 2 + 1/(2?3)?n(n - 1)(n - 2)a n-3 b 3 +…+ b n ,

it can be proven that

So if x receives an increment Δ x, That f(x+Δ x) = (x + Δ x)n, and therefore

Prove formulas 3 and 5 yourself.

Theorem. If the function at some point x = x 0 has a (finite) derivative , That

1) the increment of a function can be represented as

or, in short, , Where a is a quantity depending on D x and with it tending to zero, i.e. ;

2) the function at this point is necessarily continuous.

Proof. 1) According to the definition of derivative, . Using the theorem on the representation of a function that has a limit in the form of the sum of this limit and is infinitesimal, we write

, Where .

Determining from here D y, we arrive at formula (3.6).

2) To prove the continuity of the function, consider expression (3.6). At D x®0 the sum on the right side of (3.6) goes to zero. Hence, , or , which means that the function at the point x 0 is continuous.

From the proven theorem it follows that a function that has a derivative at a given point will be continuous at this point. However, a function that is continuous at a given point does not always have a derivative at that point. Yes, at the point x 0 = 1 function y =|x– 1| is continuous, but has no derivative at this point. This means that this condition is only necessary.

Derivative of a complex function

Theorem. Let 1) function v = j(x) has at some point x derivative, 2) function y = f(v) has at the corresponding point v derivative Then the complex function y = f(j(x)) at the mentioned point X will also have a derivative equal to the product of the derivatives of the functions f(v) And j(x): [f(j(x)) ]" = or shorter

Proof. Let's add X arbitrary increment Δ X; let Δ v– the corresponding increment of the function v = j(x) and finally Δ at– function increment y = f(v), caused by the increment Δ v. Let us use relation (3.6), which, replacing x on v, we rewrite it in the form (a depends on Δ v and tends to zero along with it). Dividing it term by term into D x, we get

If D x tend to zero, then, according to (3.6) (provided that y = v), will tend to zero and Δ v, and then, as we know, the dependence on Δ will also tend to zero v magnitude a. Therefore there is a limit

which is the desired derivative.

Thus, The derivative of a complex function is equal to the product of the derivative of the outer function and the derivative of the inner function.

The case of a complex function obtained as a result of several superpositions is resolved by sequential application of rule (3.7). So, if y = f(u), u = j(v), v = y(x), That

Examples. 1. Let y = log a sin x,in other words, y = log a v, Where v = sin x. According to rule (3.7)

2. , i.e. y = e u,u = v 2 , v = sin x. According to rule (3.8)

1.7. The derivative is exponential– power function

Let u = u(x) > 0 and v = v(x) – functions that have derivatives at a fixed point x. Let's find the derivative of the function y = u v. Taking logarithm of this equality, we get: ln y = v ln u.

Let us differentiate both sides of this equality with respect to x:

From here, or

Thus, the derivative of an exponential power function consists of two terms: the first term is obtained if, during differentiation, we assume that And there is a function from X, A v there is a constant (i.e. consider u v as a power function); the second term is obtained if we assume that v there is a function from X, A u = const(i.e. consider u v as an exponential function).

Examples. 1. If y = x tan x, then, assuming u = x,v = tan x,according to (3.9) we have

= tg x x tg x – 1 + x tg x ln x sec 2 x.

The technique used in this case to find the derivative and consists in first finding the derivative of the logarithm of the function in question, is widely used in differentiating functions: when finding the derivative of a function, these functions are first logarithmized, and then from the equality obtained after differentiating the logarithm of the function, the derivative is determined functions. This operation is called logarithmic differentiation.

2. You need to find the derivative of the function

Taking logarithms, we find:

ln y = 2ln( x+ 1) + log( x– 1) – 3 ln( x+ 4) – x.

Let's differentiate both sides of the last equality:

Multiplying by at and substituting instead of at, we get.

3 Definition of the derivative of a function at a point Let the function f(x) be defined in some neighborhood of the point x 0. DEFINITION. If there is a (finite) limit of the relation then f(x) is called the differentiable point x 0, and the limit itself is called the derivative of the function f(x) at the point x 0 and is denoted by f "(x 0), that is, Let's denote x = x – x 0 is the increment of the argument when moving from point x 0 to point x, and y = f(x 0 + x) – f(x 0) is the corresponding increment of the function. Then the derivative of the function f(x) at point x 0 is the limit of the ratio of the increment of the function to the argument increment that caused it, when the argument increment tends to zero.

4 Example 1. Let us give examples of calculating the derivatives of some of the simplest elementary functions, based on the definition of the derivative. y = a x (0 0. Assuming that | x | 0 is an arbitrary point, then 0.Assuming that | x | 0 is an arbitrary point, then">

0.Assuming that | x | 0 is an arbitrary point, then Example 4. y = sinx, x R. Take x 0 R and calculate the increment of the function at this point: So (sinx) = cosx, x R." title="5 Example 3. Let's take x 0 > 0. Assuming that | x | 0 is an arbitrary point, then Example 4. y = sinx, x R. Take x 0 R and calculate the increment of the function at this point: So (sinx) = cosx, x R." class="link_thumb"> 5 !} 5 Example 3. Take x 0 > 0. Assuming that | x | 0 is an arbitrary point, then Example 4. y = sinx, x R. Take x 0 R and calculate the increment of the function at this point: So (sinx) = cosx, x R. 0.Assuming that | x | 0 is an arbitrary point, then Example 4. y = sinx, x R. Take x 0 R and calculate the increment of the function at this point: So (sinx) = cosx, x R."> 0. Assuming that | x | 0 – arbitrary point, then Example 4. y = sinx, x R. Take x 0 R and calculate the increment of the function at this point: So (sinx) = cosx, x R."> 0. Assuming that | x | 0 is an arbitrary point, then Example 4. y = sinx, x R. Take x 0 R and calculate the increment of the function at this point: So (sinx) = cosx, x R." title="5 Example 3. Let's take x 0 > 0. Assuming that | x | 0 is an arbitrary point, then Example 4. y = sinx, x R. Take x 0 R and calculate the increment of the function at this point: So (sinx) = cosx, x R."> title="5 Example 3. Take x 0 > 0. Assuming that | x | 0 is an arbitrary point, then Example 4. y = sinx, x R. Take x 0 R and calculate the increment of the function at this point: So (sinx) = cosx, x R."> !}

6 THEOREM. If a function f(x) is differentiable at a point x 0, then it is continuous at that point. Proof. Let there exist Then From here we get that f (x) – f (x 0) = f "(x 0) (x – x 0) + (x – x 0)α(x) for x x 0. That is, f( x) is continuous at the point x 0. Continuity of the differentiable function (1)

7 NOTE. The continuity of a function at a point is not a sufficient condition for the existence of a derivative at that point. Example 5. f(x) = x. Let us study the behavior of f (x) in the vicinity of x 0 = 0. Here f (x) f (0) = 0 at x 0. That is the function is continuous at the point x 0 = 0. Consider x y 0 The limit does not exist, since So, the function f (x) = x does not have a derivative at the point x = 0, although it is continuous at this point

8 Example x y 0 at x 0. at x 0. That is f(x) is continuous at the point x = 0. That is, f(x) has no derivative at the point x = 0 and, therefore, is not differentiable at this point. Let us study the behavior of f (x) in the vicinity of the point x = 0.

9 Let the function y = f(x) be differentiable at the point x 0. Then, according to (1), its increment at the point x 0 can be written as y = f(x 0 + x) – f(x 0) = f ( x 0) x + o(x) at x. The differential of the function f (x 0) x is the main linear relative to x part of the increment of the function y = f(x) at the point x 0 is called the differential of the function at the point x 0 with the increment x and is denoted df(x 0 ; x) or df(x 0 ) or df or dу. y = f(x 0 + x) – f(x 0) = df(x 0; x) + o(x) at x. DEFINITION. The main part of the increment, linear with respect to x. An infinitesimal of a higher order than x. Now the function increment can be written like this:

10 NOTE. The increment x is often denoted by the symbol dx and is called the differential of the independent variable. Thus, the differential of a function at the point x 0 can be written in the form df(x 0) = f "(x 0) dx. If a function is differentiable at each point of a certain interval, then its differential dy is a function of x and dx: dy = f "(x)dx. From here, in particular, we obtain an expression for the derivative. That is, the derivative can be considered as the ratio of the differential of a function to the differential of the independent variable.

11 Geometric meaning of derivative and differential Let the function y = f(x) be defined in U(x 0) and differentiable at the point x 0. М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + y 0 L – secant L 0 – tangent x y = f(x 0 + x) – f(x 0) at x due to the continuity of the function. The tangent to the graph of the function y = f(x) at point M 0 is the limiting position of the secant L at x. y If the function is differentiable at the point x 0, then in the secant equation y/ x f (x 0) at x and the tangent equation has the form y = y 0 + f (x 0) (x – x 0).

12 М0М0 М x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) for x 0 L0L0 tg = f (x 0) If y/ x for x, then the straight line x = x 0 resulting from the secant equation is called the vertical tangent to the graph of the function at point M 0. From the tangent equation we obtain y – y 0 = f (x 0) (x – x 0) = df (x 0) – increment of the ordinate of the tangent when moving from point x 0 to point x. The normal to the graph of a function at point M 0 is a straight line perpendicular to the tangent passing through point M 0. Its equation has the form y = y 0 – 1/f (x 0) (x – x 0). L 1 – normal

13 Physical applications of the derivative and differential If S(t) is the path traveled by a material point in time t, then S "(t) is the instantaneous speed of the material point, and dS = S "(t)dt is the distance that the material point would travel for the period of time from t to t + dt, if it were moving at a speed equal to the instantaneous speed at the moment t. If Q(t) is the amount of electricity flowing through the cross section of the conductor at time t, then Q "(t) = I is the current strength. If N(t) is the amount of substance formed at time t during a chemical reaction, then N "(t) – rate of chemical reaction.

PROPERTIES OF FUNCTIONS CONTINUOUS ON AN INTERVIEW

Let's consider some properties of functions continuous on an interval. We present these properties without proof.

Function y = f(x) called continuous on the segment [a, b], if it is continuous at all internal points of this segment, and at its ends, i.e. at points a And b, is continuous on the right and left, respectively.

Theorem 1. A function continuous on the interval [ a, b], at least at one point of this segment takes the greatest value and at least at one point the smallest.

The theorem states that if a function y = f(x) is continuous on the interval [ a, b], then there is at least one point x 1 Î [ a, b] such that the value of the function f(x) at this point will be the largest of all its values on this segment: f(x 1) ≥ f(x). Similarly, there is such a point x 2, in which the function value will be the smallest of all values on the segment: f(x 1) ≤ f(x).

It is clear that there may be several such points; for example, the figure shows that the function f(x) takes the smallest value at two points x 2 And x 2 ".

Comment. The statement of the theorem can become incorrect if we consider the value of the function on the interval ( a, b). Indeed, if we consider the function y = x on (0, 2), then it is continuous on this interval, but does not reach either the largest or the smallest values in it: it reaches these values at the ends of the interval, but the ends do not belong to our domain.

Also, the theorem ceases to be true for discontinuous functions. Give an example.

Consequence. If the function f(x) is continuous on [ a, b], then it is limited on this segment.

Theorem 2. Let the function y = f(x) is continuous on the interval [ a, b] and at the ends of this segment takes values of different signs, then there is at least one point inside the segment x = C, in which the function goes to zero: f(C)= 0, where a< C< b

This theorem has a simple geometric meaning: if the points of the graph of a continuous function y = f(x), corresponding to the ends of the segment [ a, b] lie on opposite sides of the axis Ox, then this graph intersects the axis at at least one point of the segment Ox. Discontinuous functions may not have this property.

This theorem admits the following generalization.

Theorem 3 (intermediate value theorem). Let the function y = f(x) is continuous on the interval [ a, b] And f(a) = A, f(b) = B. Then for any number C, concluded between A And B, there is such a point inside this segment CÎ [ a, b], What f(c) = C.

This theorem is geometrically obvious. Consider the graph of the function y = f(x). Let f(a) = A, f(b) = B. Then any straight line y = C, Where C– any number between A And B, will intersect the graph of the function at least at one point. The abscissa of the intersection point will be that value x = C, at which f(c) = C.

Thus, a continuous function, moving from one value to another, necessarily passes through all intermediate values. In particular:

Consequence. If the function y = f(x) is continuous over a certain interval and takes the largest and smallest values, then on this interval it takes at least once any value contained between its smallest and largest values.

DERIVATIVE AND ITS APPLICATIONS. DEFINITION OF DERIVATIVE

Let us have some function y=f(x), defined on some interval. For each argument value x from this interval the function y=f(x) has a certain meaning.

Consider two argument values: initial x 0 and new x.

Difference x–x 0 is called by incrementing the argument x at the point x 0 and is denoted Δx. Thus, Δx = x – x 0 (the argument increment can be either positive or negative). From this equality it follows that x=x 0 +Δx, i.e. the initial value of the variable has received some increment. Then, if at the point x 0 function value was f(x 0 ), then at a new point x the function will take the value f(x) = f(x 0 +Δx).

Difference y–y 0 = f(x) – f(x 0 ) called function increment y = f(x) at the point x 0 and is indicated by the symbol Δy. Thus,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Typically the initial value of the argument x 0 is considered fixed, and the new value x– variable. Then y 0 = f(x 0 ) turns out to be constant, and y = f(x)– variable. Increments Δy And Δx will also be variables and formula (1) shows that Dy is a function of a variable Δx.

Let's create the ratio of the increment of the function to the increment of the argument

Let us find the limit of this ratio at Δx→0. If this limit exists, then it is called the derivative of this function f(x) at the point x 0 and denote f "(x 0). So,

Derivative this function y = f(x) at the point x 0 is called the limit of the function increment ratio Δ y to the argument increment Δ x, when the latter arbitrarily tends to zero.

Note that for the same function the derivative at different points x can take on different values, i.e. the derivative can be considered as a function of the argument x. This function is designated f "(x)

The derivative is denoted by the symbols f "(x),y", . The specific value of the derivative at x = a denoted by f "(a) or y "| x=a.

The operation of finding the derivative of a function f(x) is called differentiation of this function.

To directly find the derivative by definition, you can use the following: rule of thumb:

Examples.

MECHANICAL SENSE OF DERIVATIVE

It is known from physics that the law of uniform motion has the form s = v t, Where s– the path traveled to the moment of time t, v– speed of uniform motion.

However, because Most movements occurring in nature are uneven, then in general the speed, and, consequently, the distance s will depend on time t, i.e. will be a function of time.

So, let a material point move in a straight line in one direction according to the law s=s(t).

Let's mark a certain point in time t 0 . At this point the point has passed the path s=s(t 0 ). Let's determine the speed v material point at a moment in time t 0 .

To do this, let's consider some other point in time t 0 + Δ t. It corresponds to the traveled path s =s(t 0 + Δ t). Then over a period of time Δ t the point has traveled the path Δs =s(t 0 + Δ t)–s(t).

Let's consider the attitude. It is called the average speed in the time interval Δ t. The average speed cannot accurately characterize the speed of movement of a point at the moment t 0 (because the movement is uneven). In order to more accurately express this true speed using the average speed, you need to take a shorter period of time Δ t.

So, the speed of movement at a given moment in time t 0 (instantaneous speed) is the limit of average speed in the interval from t 0 to t 0 +Δ t, when Δ t→0:

those. uneven speed this is the derivative of the distance traveled with respect to time.

GEOMETRICAL MEANING OF DERIVATIVE

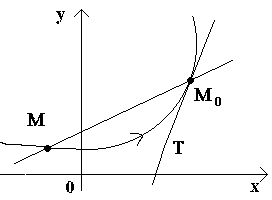
Let us first introduce the definition of a tangent to a curve at a given point.

Let us have a curve and a fixed point on it M 0(see figure). Consider another point M this curve and draw a secant M 0 M. If the point M begins to move along the curve, and the point M 0 remains motionless, then the secant changes its position. If, with unlimited approximation of the point M along a curve to a point M 0 on any side the secant tends to occupy the position of a certain straight line M 0 T, then straight M 0 T called the tangent to the curve at a given point M 0.

That., tangent to the curve at a given point M 0 called the limit position of the secant M 0 M when point M tends along the curve to a point M 0.

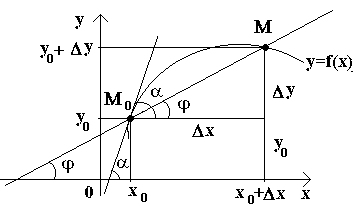
Let us now consider the continuous function y=f(x) and the curve corresponding to this function. At some value X 0 function takes value y 0 =f(x 0). These values x 0 and y 0 on the curve corresponds to a point M 0 (x 0 ; y 0). Let's give the argument x 0 increment Δ X. The new value of the argument corresponds to the incremented value of the function y 0 +Δ y=f(x 0 –Δ x). We get the point M(x 0+Δ x; y 0+Δ y). Let's draw a secant M 0 M and denote by φ the angle formed by a secant with the positive direction of the axis Ox. Let's create a relation and note that .

If now Δ x→0, then due to the continuity of the function Δ at→0, and therefore the point M, moving along a curve, approaches the point without limit M 0. Then the secant M 0 M will tend to take the position of a tangent to the curve at the point M 0, and the angle φ→α at Δ x→0, where α denotes the angle between the tangent and the positive direction of the axis Ox. Since the function tan φ continuously depends on φ for φ≠π/2, then for φ→α tan φ → tan α and, therefore, the slope of the tangent will be:

those. f "(x)= tg α .

Thus, geometrically y "(x 0) represents the slope of the tangent to the graph of this function at the point x 0, i.e. for a given argument value x, the derivative is equal to the tangent of the angle formed by the tangent to the graph of the function f(x) at the appropriate point M 0 (x; y) with positive axis direction Ox.

Example. Find the slope of the tangent to the curve y = x 2 at point M(-1; 1).

We have already seen earlier that ( x 2)" = 2X. But the angular coefficient of the tangent to the curve is tan α = y"| x=-1 = – 2.

DIFFERENTIABILITY OF FUNCTIONS. CONTINUITY OF DIFFERENTIABLE FUNCTION

Function y=f(x) called differentiable at some point x 0 if it has a certain derivative at this point, i.e. if the limit of the relationship exists and is finite.

The following theorem is valid, establishing the connection between differentiable and continuous functions.

Theorem. If the function y=f(x) differentiable at some point x 0, then it is continuous at this point.

Thus, from the differentiability of a function, its continuity follows.

Proof. If , That

where α is an infinitesimal quantity, i.e. a quantity tending to zero as Δ x→0. But then

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 at Δ x→0, i.e. f(x) – f(x 0)→0 at x→x 0 , which means that the function f(x) continuous at a point x 0 . Q.E.D.

Consider the points in the figure a, b, c.

At the point a at Δ x→0 the ratio has no limit (since the one-sided limits are different for Δ x→0–0 and Δ x→0+0). At the point A graph there is no defined tangent, but there are two different one-way tangents with slopes To 1 and To 2. This type of point is called corner point.

At the point b at Δ x The →0 ratio is a constant sign infinitely large quantity. The function has infinite derivative. At this point the graph has a vertical tangent. Point type – “inflection point” of a vertical tangent.

At the point c one-sided derivatives are infinitely large quantities of different signs. At this point the graph has two merged vertical tangents. Type – “return point” with a vertical tangent – a special case of a corner point.

Derivative. Continuity of a function having a derivative Properties of functions continuous on an interval

Password recovery