Integral with an infinite integration interval. Method for solving an improper integral with an infinite lower limit

Improper integrals of the first kind. In essence, this is the same definite integral, but in cases where the integrals have infinite upper or lower limits of integration, or both limits of integration are infinite.

Improper integrals of the second kind. In essence, this is the same definite integral, but in cases where the integral is taken from unbounded functions, the integrand at a finite number of points does not have a finite segment of integration, turning to infinity.

For comparison. When introducing the concept of a definite integral, it was assumed that the function f(x) is continuous on the interval [ a, b], and the integration segment is finite, that is, it is limited by numbers, and not by infinity. Some tasks lead to the need to abandon these restrictions. This is how improper integrals appear.

Geometric meaning of the improper integral It turns out quite simply. In the case when the graph of a function y = f(x) is above the axis Ox, the definite integral expresses the area of ​​a curvilinear trapezoid bounded by a curve y = f(x) , x-axis and ordinates x = a , x = b. In turn, the improper integral expresses the area of ​​an unlimited (infinite) curvilinear trapezoid enclosed between the lines y = f(x) (in the picture below - red), x = a and the abscissa axis.

Improper integrals are defined similarly for other infinite intervals:

The area of ​​an infinite curved trapezoid can be a finite number, in which case the improper integral is called convergent. The area can also be infinity, and in this case the improper integral is called divergent.

Using the limit of an integral instead of the improper integral itself. In order to evaluate the improper integral, you need to use the limit of the definite integral. If this limit exists and is finite (not equal to infinity), then the improper integral is called convergent, and otherwise - divergent. What a variable tends to under the limit sign depends on whether we are dealing with an improper integral of the first kind or of the second kind. Let's find out about this now.

Improper integrals of the first kind - with infinite limits and their convergence

Improper integrals with infinite upper limit

So, writing an improper integral differs from the usual definite integral in that the upper limit of integration is infinite.

Definition. An improper integral with an infinite upper limit of integration of a continuous function f(x) in the interval from a before ∞ the limit of the integral of this function with the upper limit of integration is called b and the lower limit of integration a provided that the upper limit of integration grows without limit, i.e.

.

If this limit exists and is equal to some number rather than infinity, then an improper integral is called convergent, and the number to which the limit is equal is taken as its value. Otherwise an improper integral is called divergent and no meaning is attributed to it.

Example 1. Calculate improper integral(if it converges).

Solution. Based on the definition of the improper integral, we find

Since the limit exists and is equal to 1, then this improper integral converges and is equal to 1.

In the following example, the integrand is almost the same as in example 1, only the degree x is not two, but the letter alpha, and the task is to study the improper integral for convergence. That is, the question remains to be answered: at what values ​​of alpha does this improper integral converge, and at what values ​​does it diverge?

Example 2. Examine the improper integral for convergence(the lower limit of integration is greater than zero).

Solution. Let us first assume that , then

In the resulting expression, we move to the limit at:

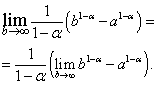
It is easy to see that the limit on the right side exists and is equal to zero when , that is , and does not exist when , that is .

In the first case, that is, when . If , then and doesn't exist.

The conclusion of our study is as follows: this improper integral converges at and diverges at .

Applying the Newton-Leibniz formula to the type of improper integral being studied , you can derive the following formula, which is very similar to it:

.

This is a generalized Newton-Leibniz formula.

Example 3. Calculate improper integral(if it converges).

The limit of this integral exists:

The second integral, making up the sum expressing the original integral:

The limit of this integral also exists:

.

We find the sum of two integrals, which is also the value of the original improper integral with two infinite limits:

Improper integrals of the second kind - from unbounded functions and their convergence

Let the function f(x) given on the segment from a before b and is unlimited on it. Suppose that the function goes to infinity at the point b , while at all other points of the segment it is continuous.

Definition. An improper integral of a function f(x) on the segment from a before b the limit of the integral of this function with the upper limit of integration is called c , if when striving c To b the function increases without limit, and at the point x = b function not defined, i.e.

.

If this limit exists, then the improper integral of the second kind is called convergent, otherwise it is called divergent.

Using the Newton-Leibniz formula, we derive.

Are you here now? =) No, I wasn’t trying to intimidate anyone, it’s just that the topic of improper integrals is a very good illustration of how important it is not to neglect higher mathematics and other exact sciences. Everything you need to learn the lesson is on the website - in a detailed and accessible form, if you wish...

So, let's start with. Figuratively speaking, an improper integral is an “advanced” definite integral, and in fact there are not so many difficulties with them, and besides, the improper integral has a very good geometric meaning.

What does it mean to evaluate an improper integral?

Calculate improper integral - this means finding the NUMBER(exactly the same as in the definite integral), or prove that it diverges(that is, you end up with infinity instead of a number).

There are two types of improper integrals.

Improper integral with infinite limit(s) of integration

Sometimes such an improper integral is called improper integral of the first kind. In general, an improper integral with an infinite limit most often looks like this: . How is it different from a definite integral? At the upper limit. It is endless: .

Less common are integrals with an infinite lower limit or with two infinite limits: , and we will look at them later - when you get the hang of it :)

Well, now let’s look at the most popular case. In the vast majority of examples, the integrand function continuous in between, and this one important fact should be checked first! Because if there are gaps, then there are additional nuances. For definiteness, let us assume that even then the typical curved trapezoid will look like this:

Note that it is infinite (not bounded on the right), and improper integral numerically equal to its area. The following options are possible:

1) The first thought that comes to mind: “since the figure is infinite, then ", in other words, the area is also infinite. It may be so. In this case they say that the improper integral diverges.

2) But. As paradoxical as it may sound, the area of ​​an infinite figure can be equal to... a finite number! For example: . Could this be true? Easily. In the second case, the improper integral converges.

3) About the third option a little later.

In what cases does an improper integral diverge and in what cases does it converge? This depends on the integrand, and we'll look at specific examples very soon.

What happens if an infinite curved trapezoid is located below the axis? In this case, the improper integral (diverges) or is equal to a finite negative number.

Thus, improper integral can be negative.

Important! When you are given ANY improper integral to solve, then, generally speaking, there is no talk about any area and there is no need to build a drawing. I explained the geometric meaning of the improper integral only to make it easier to understand the material.

Since the improper integral is very similar to the definite integral, let us remember the Newton-Leibniz formula: . In fact, the formula is also applicable to improper integrals, only it needs to be slightly modified. What is the difference? At the infinite upper limit of integration: . Probably, many guessed that this already smacks of the application of the theory of limits, and the formula will be written like this: .

What is the difference from a definite integral? Nothing special! As in the definite integral, you need to be able to find the antiderivative function (indefinite integral), and be able to apply the Newton-Leibniz formula. The only thing that has been added is the calculation of the limit. Whoever has a bad time with them, learn a lesson Function limits. Examples of solutions, because it’s better late than in the army.

Let's look at two classic examples:

Example 1

For clarity, I will draw a drawing, although, I emphasize once again, on practice There is no need to build drawings in this task.

The integrand function is continuous on the half-interval, which means that everything is fine and the improper integral can be calculated by the “standard” method.

Application of our formula and the solution to the problem looks like this:

That is, the improper integral diverges, and the area of ​​the shaded curved trapezoid is equal to infinity.

In the example considered, we have the simplest table integral and the same technique for applying the Newton-Leibniz formula as in the definite integral. But this formula will be applied under the sign of the limit. Instead of the usual letter of a “dynamic” variable, the letter “be” appears. This should not confuse or baffle, because any letter is no worse than the standard “X”.

If you do not understand why at , then this is very bad, either you do not understand the simplest limits (and generally do not understand what a limit is), or you do not know what the graph of a logarithmic function looks like. In the second case, attend a lesson Graphs and properties of elementary functions.

When solving improper integrals, it is very important to know what the graphs of basic elementary functions look like!

The finished task should look something like this:

“

! When preparing an example, we always interrupt the solution and indicate what happens to the integrand – is it continuous on the interval of integration or not?. With this we identify the type of improper integral and justify further actions.

Example 2

Calculate the improper integral or establish its divergence.

Let's make the drawing:

First, we note the following: the integrand is continuous on the half-interval. Hood. We solve using the formula :

(1) We take the simplest integral of a power function (this special case is in many tables). It is better to immediately move the minus sign beyond the limit sign so that it does not get in the way in further calculations.

(2) We substitute the upper and lower limits using the Newton-Leibniz formula.

(3) We indicate that at (Gentlemen, this should have been understood a long time ago) and simplify the answer.

Here the area of ​​an infinite curved trapezoid is a finite number! Unbelievable but true.

The finished example should look something like this:

“

The integrand function is continuous on

“

What to do if you come across an integral like - with break point on the integration interval? This means there is a typo in the example. (Most likely), or about an advanced level of training. In the latter case, due to additivity properties, we should consider two improper integrals on intervals and then deal with the sum.

Sometimes, due to a typo or intent, an improper integral may not exist at all, so, for example, if you put the square root of “x” in the denominator of the above integral, then part of the integration interval will not be included in the domain of definition of the integrand at all.

Moreover, the improper integral may not exist even with all the “apparent well-being”. Classic example: . Despite the definiteness and continuity of the cosine, such an improper integral does not exist! Why? It's very simple because:
- does not exist appropriate limit.

And such examples, although rare, do occur in practice! Thus, in addition to convergence and divergence, there is also a third outcome of the solution with a valid answer: “there is no improper integral.”

It should also be noted that the strict definition of an improper integral is given precisely through the limit, and those who wish can familiarize themselves with it in the educational literature. Well, we continue the practical lesson and move on to more meaningful tasks:

Example 3

Calculate the improper integral or establish its divergence.

First, let's try to find the antiderivative function (indefinite integral). If we fail to do this, then naturally we will not be able to solve the improper integral either.

Which of the table integrals is the integrand similar to? It reminds me of an arctangent: . These considerations suggest that it would be nice to have a square in the denominator. This is done by replacement.

Let's replace:

The indefinite integral has been found; in this case, it makes no sense to add a constant.

It is always useful to check the draft, that is, differentiate the result obtained:

The original integrand has been obtained, which means that the indefinite integral has been found correctly.

Now we find the improper integral:

(1) We write the solution in accordance with the formula . It is better to immediately move the constant beyond the limit sign so that it does not interfere with further calculations.

(2) We substitute the upper and lower limits in accordance with the Newton-Leibniz formula. Why at ? See the arctangent graph in the already recommended article.

(3) We get the final answer. A fact that is useful to know by heart.

Advanced students may not find the indefinite integral separately and not use the replacement method, but rather use the method of substituting the function under the differential sign and solving the improper integral “immediately.” In this case, the solution should look something like this:

“

The integrand is continuous on .

“

Example 4

Calculate the improper integral or establish its divergence.

! This is a typical example, and similar integrals are found very often. Work it out well! The antiderivative function here is found using the method of selecting a complete square; more details on the method can be found in the lesson Integrating Some Fractions.

Example 5

Calculate the improper integral or establish its divergence.

This integral can be solved in detail, that is, first find the indefinite integral by making a change of variable. Or you can solve it “immediately” - by subsuming the function under the differential sign. Who has any mathematical training?

Complete solutions and answers at the end of the lesson.

Examples of solutions to improper integrals with an infinite lower limit of integration can be found on the page Efficient methods for solving improper integrals. There we also analyzed the case when both limits of integration are infinite.

Improper integrals of unbounded functions

Or improper integrals of the second kind. Improper integrals of the second kind are insidiously “encrypted” under the usual definite integral and look exactly the same: But, unlike the definite integral, the integrand suffers an infinite discontinuity (does not exist): 1) at the point , 2) or at the point , 3) ​​or at both points at once, 4) or even on the integration segment. We will look at the first two cases; for cases 3-4 at the end of the article there is a link to an additional lesson.

Just an example to make it clear: . It seems to be a definite integral. But in fact, this is an improper integral of the second kind; if we substitute the value of the lower limit into the integrand, then our denominator goes to zero, that is, the integrand simply does not exist at this point!

In general, when analyzing an improper integral you always need to substitute both integration limits into the integrand. In this regard, let's check the upper limit: . Everything is fine here.

The curvilinear trapezoid for the type of improper integral under consideration fundamentally looks like this:

Here everything is almost the same as in the integral of the first kind.

Our integral is numerically equal to the area of ​​the shaded curved trapezoid, which is not bounded from above. In this case, there can be two options*: the improper integral diverges (the area is infinite) or the improper integral is equal to a finite number (that is, the area of ​​an infinite figure is finite!).

* by default we usually assume that the improper integral exists

All that remains is to modify the Newton-Leibniz formula. It is also modified with the help of a limit, but the limit no longer tends to infinity, but to the value on the right. It is easy to follow from the drawing: along the axis we must approach the breaking point infinitely close on right.

Let's see how this is implemented in practice.

Example 6

Calculate the improper integral or establish its divergence.

The integrand has an infinite discontinuity at a point (don’t forget to check verbally or on a draft that everything is fine with the upper limit!)

First, let's calculate the indefinite integral:

Replacement:

If you have any difficulties with replacement, please refer to the lesson Substitution method in indefinite integral.

Let's calculate the improper integral:

(1) What's new here? There is practically nothing in terms of solution technology. The only thing that has changed is the entry under the limit icon: . The addition means that we are striving for the value on the right (which is logical - see the graph). Such a limit in the theory of limits is called one-sided limit. In this case we have right-hand limit.

(2) We substitute the upper and lower limits using the Newton-Leibniz formula.

(3) Let's deal with at . How to determine where an expression is going? Roughly speaking, you just need to substitute the value into it, substitute three quarters and indicate that . Let's comb the answer.

In this case, the improper integral is equal to a negative number. There is no crime in this, just the corresponding curved trapezoid is located under the axis.

And now two examples for independent solutions.

Example 7

Calculate the improper integral or establish its divergence.

Example 8

Calculate the improper integral or establish its divergence.

If the integrand does not exist at the point

An infinite curved trapezoid for such an improper integral fundamentally looks like this.

Definite integral as the limit of the integral sum

can exist (i.e. have a certain final value) only if the conditions are met

If at least one of these conditions is violated, then the definition loses its meaning. Indeed, in the case of an infinite segment, for example [ a; ) it cannot be divided into P parts of finite length
, which, moreover, would tend to zero with an increase in the number of segments. In the case of unlimited at some point With[a; b] the requirement for arbitrary point selection is violated on partial segments – cannot be selected =With, since the value of the function at this point is undefined. However, even for these cases it is possible to generalize the concept of a definite integral by introducing another passage to the limit. Integrals over infinite intervals and over discontinuous (unbounded) functions are called not your own.

Definition.

Let the function
is defined on the interval [ a; ) and is integrable on any finite interval [ a; b], i.e. exists
for anyone b > a. Type limit
called improper integral first kind (or an improper integral over an infinite interval) and denote
.

Thus, by definition,
=
.

If the limit on the right exists and is finite, then the improper integral
called convergent . If this limit is infinite, or does not exist at all, then they say that the improper integral diverges .

Similarly, we can introduce the concept of an improper integral of the function
along the interval (–; b]:

=
.

And the improper integral of the function
over the interval (–; +) is defined as the sum of the integrals introduced above:

=
+
,

Where A– arbitrary point. This integral converges if both terms converge, and diverges if at least one of the terms diverges.

From a geometric point of view, the integral
,
, determines the numerical value of the area of ​​an infinite curvilinear trapezoid bounded above by the graph of the function
, left – straight
, from below – by the OX axis. The convergence of the integral means the existence of a finite area of ​​such a trapezoid and its equality to the limit of the area of ​​a curvilinear trapezoid with a movable right wall
.

To the case of an integral with an infinite limit, we can generalize Newton-Leibniz formula:

=
= F( + ) – F( a),

where F( + ) =
. If this limit exists, then the integral converges, otherwise it diverges.

We considered a generalization of the concept of a definite integral to the case of an infinite interval.

Let us now consider a generalization for the case of an unbounded function.

Definition

Let the function
is defined on the interval [ a; b), is unlimited in some neighborhood of the point b, and is continuous on any interval
, where >0 (and, therefore, integrable on this interval, i.e.
exists). Type limit
called improper integral of the second kind (or an improper integral of an unbounded function) and is denoted
.

Thus, the improper integral of the unbounded at the point b functions exist by definition

=
.

If the limit on the right exists and is finite, then the integral is called convergent. If there is no finite limit, then the improper integral is called divergent.

Similarly, we can define the improper integral of the function
having an infinite discontinuity at the point A:

=
.

If the function
has an infinite gap at the interior point With
, then the improper integral is defined as follows

=
+
=
+
.

This integral converges if both terms converge, and diverges if at least one term diverges.

From a geometric point of view, the improper integral of an unbounded function also characterizes the area of ​​an unbounded curved trapezoid:

Since an improper integral is derived by passing to the limit from a definite integral, all the properties of a definite integral can be transferred (with appropriate refinements) to improper integrals of the first and second kind.

In many problems that lead to improper integrals, it is not necessary to know what this integral is equal to, it is enough just to verify its convergence or divergence. For this they use signs of convergence. Signs of convergence of improper integrals:

1) Comparison sign.

Let it be for everyone X

. Then if
converges, then converges
, and

. If
diverges, then diverges and
.

2) If converges
, then converges and
(the last integral in this case is called absolutely convergent).

The signs of convergence and divergence of improper integrals of unbounded functions are similar to those formulated above.

Examples of problem solving.

Example 1.

A)
; b)
; V)

G)
; d)
.

Solution.

a) By definition we have:

.

b) Likewise

Therefore, this integral converges and is equal to .

c) By definition
=
+
, and A– arbitrary number. Let's put in our case
, then we get:

This integral converges.

This means that this integral diverges.

e) Let's consider
. To find the antiderivative of the integrand, it is necessary to apply the method of integration by parts. Then we get:

Since neither
, neither
do not exist, then does not exist and

Therefore, this integral diverges.

Example 2.

Investigate the convergence of the integral depending on the P.

Solution.

At
we have:

If
, That
And . Therefore, the integral diverges.

If
, That
, A
, Then

= ,

Therefore, the integral converges.

If
, That

therefore, the integral diverges.

Thus,

Example 3.

Calculate the improper integral or establish its divergence:

A)
; b)
; V)
.

Solution.

a) Integral
is an improper integral of the second kind, since the integrand
not limited at a point

. Then, by definition,

.

The integral converges and is equal to .

b) Consider
. Here also the integrand is not limited at the point
. Therefore, this integral is improper of the second kind and, by definition,

Therefore, the integral diverges.

c) Consider
. Integrand
suffers an infinite gap at two points:
And
, the first of which belongs to the integration interval
. Consequently, this integral is an improper integral of the second kind. Then, by definition

=

=

.

Therefore, the integral converges and is equal to
.

Improper integral with infinite integration limit

Sometimes such an improper integral is also called an improper integral of the first kind..gif" width="49" height="19 src=">.

Less common are integrals with an infinite lower limit or with two infinite limits: .

We will consider the most popular case https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? No not always. Integrandhttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">

Let us depict in the drawing the graph of the integrand function. A typical graph and curved trapezoid for this case looks like this:

Improper integralhttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", in other words, the area is also infinite. It may be so. In this case they say that the improper integral diverges.

2) But. As paradoxical as it may sound, the area of ​​an infinite figure can be equal to... a finite number! For example: .. In the second case, the improper integral converges.

What happens if an infinite curved trapezoid is located below the axis?.gif" width="217" height="51 src=">.

: .

Example 1

The integrand function https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, which means everything is fine and the improper integral can be calculated using the “standard” method.

Application of our formula https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">

That is, the improper integral diverges, and the area of ​​the shaded curved trapezoid is equal to infinity.

When solving improper integrals, it is very important to know what the graphs of basic elementary functions look like!

Example 2

Calculate the improper integral or establish its divergence.

Let's make the drawing:

First, we note the following: the integrand is continuous on the half-interval. Good..gif" width="327" height="53">

(1) We take the simplest integral of a power function (this special case is in many tables). It is better to immediately move the minus sign beyond the limit sign so that it does not get in the way in further calculations.

(2) We substitute the upper and lower limits using the Newton-Leibniz formula.

(3) We point out that https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Gentlemen, this needs to be understood a long time ago) and simplify answer.

Here the area of ​​an infinite curved trapezoid is a finite number! Unbelievable but true.

Example 3

Calculate the improper integral or establish its divergence.

The integrand is continuous on .

First, let's try to find the antiderivative function (indefinite integral).

Which of the table integrals is the integrand similar to? It reminds me of an arctangent: . These considerations suggest that it would be nice to have a square in the denominator. This is done by replacement.

Let's replace:

It is always useful to perform a check, that is, to differentiate the result obtained:

Now we find the improper integral:

(1) We write the solution in accordance with the formula . It is better to immediately move the constant beyond the limit sign so that it does not interfere with further calculations.

(2) We substitute the upper and lower limits in accordance with the Newton-Leibniz formula..gif" width="56" height="19 src=">? See the arctangent graph in the already repeatedly recommended article.

(3) We get the final answer. A fact that is useful to know by heart.

Advanced students may not find the indefinite integral separately and not use the replacement method, but rather use the method of substituting the function under the differential sign and solving the improper integral “immediately.” In this case, the solution should look something like this:

“

The integrand function is continuous at https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“

Example 4

Calculate the improper integral or establish its divergence.

! This is a typical example, and similar integrals are found very often. Work it out well! The antiderivative function is found here using the method of isolating a complete square.

Example 5

Calculate the improper integral or establish its divergence.

This integral can be solved in detail, that is, first find the indefinite integral by making a change of variable. Or you can solve it “immediately” - by subsuming the function under the differential sign..

Improper integrals of unbounded functions

Sometimes such improper integrals are called improper integrals of the second kind. Improper integrals of the second kind are insidiously “encrypted” under the usual definite integral and look exactly the same: ..gif" width="39" height="15 src=">, 2) or at point , 3) ​​or at both points at once, 4) or even on the integration segment.We will consider the first two cases, for cases 3-4 at the end of the article there is a link to an additional lesson.

Just an example to make it clear: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, then our denominator goes to zero, that is, the integrand simply does not exist at this point!

In general, when analyzing an improper integral you always need to substitute both integration limits into the integrand..jpg" alt="Improper integral, discontinuity point at the lower limit of integration" width="323" height="380">!}

Here everything is almost the same as in the integral of the first kind.
Our integral is numerically equal to the area of ​​the shaded curved trapezoid, which is not bounded from above. In this case, there can be two options: the improper integral diverges (the area is infinite) or the improper integral is equal to a finite number (that is, the area of ​​an infinite figure is finite!).

All that remains is to modify the Newton-Leibniz formula. It is also modified with the help of a limit, but the limit no longer tends to infinity, but to valuehttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> on right.

Example 6

Calculate the improper integral or establish its divergence.

The integrand has an infinite discontinuity at a point (don’t forget to check verbally or on a draft that everything is fine with the upper limit!)

First, let's calculate the indefinite integral:

Replacement:

Let's calculate the improper integral:

(1) What's new here? There is practically nothing in terms of solution technology. The only thing that has changed is the entry under the limit icon: . The addition means that we are striving for the value on the right (which is logical - see the graph). Such a limit in the theory of limits is called a one-sided limit. In this case we have a right-handed limit.

(2) We substitute the upper and lower limits using the Newton-Leibniz formula.

(3) Let's understand https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. How to determine where the expression should go? Roughly speaking, in you just need to substitute the value , substitute three quarters and indicate that .. We comb the answer.

In this case, the improper integral is equal to a negative number.

Example 7

Calculate the improper integral or establish its divergence.

Example 8

Calculate the improper integral or establish its divergence.

If the integrand does not exist at the point

An infinite curved trapezoid for such an improper integral fundamentally looks like this:

Here everything is absolutely the same, except that our limit tends to to valuehttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> we must approach infinitely close to the breaking point left.

Called Improper integral From functionF(X) with an infinite upper limit. If this limit exists and is finite, then the improper integral is called Convergent. But if it does not exist or is equal
± ¥, then this improper integral is called Divergent.

If F(X) ≥ 0 for all X ≥ A, That U improper integral (6.1) has an obvious geometric meaning, which follows from the geometric meaning (4.3) of the ordinary definite integral. Indeed, according to Fig. 5.14

(6.2)

(6.3)

Here S¥ - area infinitely extended in the direction of the axis Oh curvilinear trapezoid (Fig. 5.15). Despite its infinite extent, it can also turn out to be finite. But this can happen, according to Fig. 5.15, only in the case when Y = F(X) → 0 at X → ¥ . And even then, if the function Y = F(X) → 0 at X → ¥ fast enough.

Example 1. Find area S¥ , shown in Fig. 5.16.

,
since ln B → ¥ at B → ¥ .

So, S¥ = ¥. And this despite the fact that the function when X → ¥ . An improper integral, which means it diverges.

Example 2. Find area S¥ , shown in Fig. 5.17.

Here S¥ = 1. That is, an infinitely extended area turned out to be finite. This happened because the integrand function at X → ¥ fast enough (at least much faster than the integrand in the previous example). An improper integral (a number), which means it converges.

Example 3 . Find out whether the improper integral converges or diverges.

Solution . Let's calculate this integral:

Does not exist. This is obvious if we recall the behavior of the graph of the function Y= = Sin X(sinusoids) at X → ¥ . Thus, it does not exist, which means it diverges. However, this could not be otherwise, because the integrand function cos X does not tend to zero at X →¥ .

Note that when calculating improper integrals of type, as well as when calculating ordinary definite integrals, you can immediately apply the Newton-Leibniz formula:

Here

Really:

If the value F(¥ ) exists and is finite, then according to the Newton-Leibniz formula (6.4) the improper integral also converges.

Note. Quite analogously to integrals with an infinite upper limit, one can consider improper integrals with an infinite lower limit and even with both infinite limits of integration. That is, integrals of the form

To calculate them, you can also use the Newton-Leibniz formula.

Example 4.

So, (number), that is, this integral converges. Its value π is equal to the area S¥ the infinitely extended figure in both directions shown in Fig. 5.18.

Note that the very fact of convergence-divergence of improper integrals with infinite limits of integration does not have to be established by direct calculation of these integrals. This question can often be solved much more simply by comparing this improper integral with some other integral for which convergence-divergence has already been established.

Suppose, for example, that for everyone there is inequality F(X) £ G(X), Where Y = F(X) AND Y = G(X) - Two continuous and non-negative functions (Fig. 5.19). Then it is obvious that

From inequality (6.6) and Fig. 5.19 obviously follows the so-called Comparison test for improper integrals:

1) If (number) converges, then (number) - converges, and B 2) If - diverges, then - diverges. 3) If - diverges, then - nothing can be said about this integral. 4) If (number) - converges, then - nothing can be said about this integral.

As a function G(X) , with which this function is compared on the interval F(X), the function is often used, and the integral is used as a comparison integral, taking into account that when A > 0 and any α function is a positive and continuous function, and that

Example 5.

Solution. It's obvious that for all X Î }