The smallest value of the function f x. Largest and smallest value of a function
In July 2020, NASA launches an expedition to Mars. Spacecraft will deliver to Mars an electronic medium with the names of all registered expedition participants.
If this post solved your problem or you just liked it, share the link to it with your friends on social networks.
One of these code options needs to be copied and pasted into the code of your web page, preferably between tags and or immediately after the tag. According to the first option, MathJax loads faster and slows down the page less. But the second option automatically monitors and loads the latest versions of MathJax. If you insert the first code, it will need to be updated periodically. If you insert the second code, the pages will load more slowly, but you will not need to constantly monitor MathJax updates.
The easiest way to connect MathJax is in Blogger or WordPress: in the site control panel, add a widget designed to insert third-party JavaScript code, copy the first or second version of the download code presented above into it, and place the widget closer to the beginning of the template (by the way, this is not at all necessary , since the MathJax script is loaded asynchronously). That's all. Now learn the markup syntax of MathML, LaTeX and ASCIIMathML and you are ready to embed mathematical formulas to the web pages of your site.
Another New Year's Eve... frosty weather and snowflakes on the window glass... All this prompted me to write again about... fractals, and what Wolfram Alpha knows about it. There is an interesting article on this subject, which contains examples of two-dimensional fractal structures. Here we will look at more complex examples three-dimensional fractals.
A fractal can be visually represented (described) as a geometric figure or body (meaning that both are a set, in this case, a set of points), the details of which have the same shape as the original figure itself. That is, this is a self-similar structure, examining the details of which when magnified, we will see the same shape as without magnification. Whereas in the case of ordinary geometric figure(not a fractal), when zoomed in we will see details that have a simpler shape than the original figure itself. For example, at a high enough magnification, part of an ellipse looks like a straight line segment. This does not happen with fractals: with any increase in them, we will again see the same complex shape, which will be repeated again and again with each increase.
Benoit Mandelbrot, the founder of the science of fractals, wrote in his article Fractals and Art in the Name of Science: “Fractals are geometric shapes that are as complex in their details as they are in their general form. That is, if part of a fractal is enlarged to the size of the whole, it will appear as the whole, either exactly, or perhaps with a slight deformation."
Using this service you can find the largest and smallest value functions of one variable f(x) with the solution formatted in Word. If the function f(x,y) is given, therefore, it is necessary to find the extremum of the function of two variables. You can also find the intervals of increasing and decreasing functions.
Rules for entering functions:
Necessary condition for the extremum of a function of one variable The equation f" 0 (x *) = 0 is a necessary condition for the extremum of a function of one variable, i.e. at point x * the first derivative of the function must vanish. It identifies stationary points x c at which the function does not increase or decrease. Sufficient condition for the extremum of a function of one variable Let f 0 (x) be twice differentiable with respect to x belonging to the set D. If at the point x * the condition is satisfied:F" 0 (x *) = 0
f"" 0 (x *) > 0
Then point x * is the local (global) minimum point of the function.
If at point x * the condition is met:
F" 0 (x *) = 0
f"" 0 (x *)< 0
Then point x * is a local (global) maximum.
Example No. 1. Find the largest and smallest values of the function: on the segment.
Solution. ![]()
The critical point is one x 1 = 2 (f’(x)=0). This point belongs to the segment. (The point x=0 is not critical, since 0∉).
We calculate the values of the function at the ends of the segment and at the critical point.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Answer: f min = 5 / 2 at x=2; f max =9 at x=1
Example No. 2. Using higher order derivatives, find the extremum of the function y=x-2sin(x) .
Solution.
Find the derivative of the function: y’=1-2cos(x) . Let's find the critical points: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. We find y’’=2sin(x), calculate , which means x= π / 3 +2πk, k∈Z are the minimum points of the function; ![]() , which means x=- π / 3 +2πk, k∈Z are the maximum points of the function.
, which means x=- π / 3 +2πk, k∈Z are the maximum points of the function.
Example No. 3. Investigate the extremum function in the vicinity of the point x=0.
Solution. Here it is necessary to find the extrema of the function. If the extremum x=0, then find out its type (minimum or maximum). If among the found points there is no x = 0, then calculate the value of the function f(x=0).
It should be noted that when the derivative on each side of a given point does not change its sign, the possible situations are not exhausted even for differentiable functions: it can happen that for an arbitrarily small neighborhood on one side of the point x 0 or on both sides the derivative changes sign. At these points it is necessary to use other methods to study functions at an extremum.
Example No. 4. Divide the number 49 into two terms whose product will be greatest.
Solution. Let us denote x as the first term. Then (49-x) is the second term.
The product will be maximum: x·(49-x) → max
The figures below show where the function can reach its smallest and largest value. In the left figure the smallest and highest value are fixed at the points of local minimum and maximum of the function. In the right picture - at the ends of the segment.

If the function y = f(x) is continuous on the interval [ a, b] , then it reaches on this segment least And highest values. This, as already mentioned, can happen either at extremum points or at the ends of the segment. Therefore, to find least And the largest values of the function, continuous on the interval [ a, b], you need to calculate its values at all critical points and at the ends of the segment, and then select the smallest and largest from them.
Let, for example, you want to determine the largest value of the function f(x) on the segment [ a, b] . To do this, you need to find all its critical points lying on [ a, b] .
Critical point is the point at which a function is defined and its derivative is either zero or does not exist. Then you should calculate the values of the function at the critical points. And finally, one should compare the values of the function at critical points and at the ends of the segment ( f(a) And f(b)). The largest of these numbers will be the largest value of the function on the segment [a, b] .
Problems of finding smallest function values .
We look for the smallest and largest values of the function togetherExample 1. Find the smallest and largest values of a function ![]() on the segment [-1, 2] .
on the segment [-1, 2] .
Solution. Find the derivative of this function. Let's equate the derivative to zero () and get two critical points: and . To find the smallest and largest values of a function on a given segment, it is enough to calculate its values at the ends of the segment and at the point, since the point does not belong to the segment [-1, 2]. These function values are: , , . It follows from this that the smallest value of the function (indicated in red on the graph below), equal to -7, is achieved at the right end of the segment - at point , and the largest (also red on the graph), equal to 9, - at the critical point.

If a function is continuous in a certain interval and this interval is not a segment (but is, for example, an interval; the difference between an interval and a segment: the boundary points of the interval are not included in the interval, but the boundary points of the segment are included in the segment), then among the values of the function there may not be to be the smallest and the greatest. So, for example, the function shown in the figure below is continuous on ]-∞, +∞[ and does not have the greatest value.

However, for any interval (closed, open or infinite), the following property of continuous functions is true.
To self-check your calculations, you can use the online derivative calculator.
Example 4. Find the smallest and largest values of the function on the interval [-1, 3] .
Solution. We find the derivative of this function as the derivative of the quotient:
 .
.
We equate the derivative to zero, which gives us one critical point: . It belongs to the segment [-1, 3] . To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:

Let's compare these values. Conclusion: , equal to -5/13, at the point and the largest value, equal to 1, at the point.
We continue to look for the smallest and largest values of the function togetherThere are teachers who, on the topic of finding the smallest and largest values of a function, do not give students examples to solve that are more complex than those just discussed, that is, those in which the function is a polynomial or a fraction, the numerator and denominator of which are polynomials. But we will not limit ourselves to such examples, since among teachers there are those who like to force students to think in full (the table of derivatives). Therefore, the logarithm and trigonometric function will be used.
Example 8. Find the smallest and largest values of the function on the segment.
Solution. We find the derivative of this function as the derivative of the product:
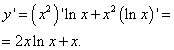
We equate the derivative to zero, which gives one critical point: . It belongs to the segment. To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:

The result of all actions: the function reaches the smallest value equal to 0 at the point and at the point and the largest value equal to e², at the point.
To self-check your calculations, you can use the online derivative calculator.
Example 9. Find the smallest and largest values of a function ![]() on the segment.
on the segment.
Solution. Find the derivative of this function:
We equate the derivative to zero:

The only critical point belongs to the segment. To find the smallest and largest values of a function on a given segment, we find its values at the ends of the segment and at the found critical point:

Conclusion: the function reaches the smallest value equal to , at the point and the largest value, equal to , at the point .
In applied extremal problems, finding the smallest (maximum) values of a function, as a rule, comes down to finding the minimum (maximum). But it is not the minimums or maximums themselves that are of greater practical interest, but those values of the argument at which they are achieved. When solving applied problems, an additional difficulty arises - composing functions that describe the phenomenon or process under consideration.
Example 10. A tank with a capacity of 4, having the shape of a parallelepiped with a square base and open at the top, needs to be tinned. What size should the tank be so that the least amount of material is used to cover it?
Solution. Let x- base side, h- tank height, S- its surface area without cover, V- its volume. The surface area of the tank is expressed by the formula, i.e. is a function of two variables. To express S as a function of one variable, we use the fact that , from where . Substituting the found expression h into the formula for S:
Let's examine this function to its extremum. It is defined and differentiable everywhere in ]0, +∞[ , and
![]() .
.
We equate the derivative to zero () and find the critical point. In addition, when the derivative does not exist, but this value is not included in the domain of definition and therefore cannot be an extremum point. So, this is the only critical point. Let's check it for the presence of an extremum using the second sufficient indication. Let's find the second derivative. When the second derivative is greater than zero (). This means that when the function reaches a minimum ![]() . Since this minimum is the only extremum of this function, it is its smallest value. So, the side of the base of the tank should be 2 m, and its height should be .
. Since this minimum is the only extremum of this function, it is its smallest value. So, the side of the base of the tank should be 2 m, and its height should be .
For self-checking during calculations, you can use
Sometimes in problems B15 there are “bad” functions for which it is difficult to find a derivative. Previously, this only happened during sample tests, but now these tasks are so common that they can no longer be ignored when preparing for the real Unified State Exam.
In this case, other techniques work, one of which is monotone.
A function f (x) is said to be monotonically increasing on the segment if for any points x 1 and x 2 of this segment the following holds:
x 1< x 2 ⇒ f (x 1 ) < f (x 2 ).
A function f (x) is said to be monotonically decreasing on the segment if for any points x 1 and x 2 of this segment the following holds:
x 1< x 2 ⇒ f (x 1 ) >f(x2).
In other words, for an increasing function, the larger x, the larger f(x). For a decreasing function the opposite is true: the larger x, the less f(x).
For example, the logarithm increases monotonically if the base a > 1, and monotonically decreases if 0< a < 1. Не забывайте про область acceptable values logarithm: x > 0.
f (x) = log a x (a > 0; a ≠ 1; x > 0)
The arithmetic square (and not only square) root increases monotonically over the entire domain of definition:
The exponential function behaves similarly to the logarithm: it increases for a > 1 and decreases for 0< a < 1. Но в отличие от логарифма, exponential function defined for all numbers, not just x > 0:
f (x) = a x (a > 0)
Finally, degrees with a negative exponent. You can write them as a fraction. They have a break point where the monotony is broken.
All these functions are never found in their pure form. They add polynomials, fractions and other nonsense, which makes it difficult to calculate the derivative. Let's look at what happens in this case.
Parabola vertex coordinatesMost often the function argument is replaced with quadratic trinomial of the form y = ax 2 + bx + c. Its graph is a standard parabola in which we are interested in:
Of greatest interest is vertex of parabola, the abscissa of which is calculated by the formula:
So, we have found the extremum point of the quadratic function. But if the original function is monotonic, for it the point x 0 will also be an extremum point. Thus, let us formulate the key rule:
The extremum points of a quadratic trinomial and the complex function in which it is included coincide. Therefore, you can look for x 0 for a quadratic trinomial, and forget about the function.
From the above reasoning, it remains unclear which point we get: maximum or minimum. However, the tasks are specifically designed so that this does not matter. Judge for yourself:
Thus, solving the problem is greatly simplified and comes down to just two steps:
At first glance, this algorithm and its rationale may seem complex. I deliberately do not post a “bare” solution diagram, since thoughtless application of such rules is fraught with errors.
Let's look at real problems from trial Unified State Exam in mathematics - exactly there this technique occurs most often. At the same time, we will make sure that in this way many B15 problems become almost oral.
Under the root stands quadratic function y = x 2 + 6x + 13. The graph of this function is a parabola with branches upward, since the coefficient a = 1 > 0.
Vertex of the parabola:
x 0 = −b /(2a ) = −6/(2 1) = −6/2 = −3
Since the branches of the parabola are directed upward, at the point x 0 = −3 the function y = x 2 + 6x + 13 takes on its minimum value.
The root increases monotonically, which means x 0 is the minimum point of the entire function. We have:
Task. Find the smallest value of the function:
y = log 2 (x 2 + 2x + 9)
Under the logarithm there is again a quadratic function: y = x 2 + 2x + 9. The graph is a parabola with branches up, because a = 1 > 0.
Vertex of the parabola:
x 0 = −b /(2a ) = −2/(2 1) = −2/2 = −1
So, at the point x 0 = −1 the quadratic function takes on its minimum value. But the function y = log 2 x is monotonic, so:
y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = ... = log 2 8 = 3
The exponent contains the quadratic function y = 1 − 4x − x 2 . Let's rewrite it in normal form: y = −x 2 − 4x + 1.
Obviously, the graph of this function is a parabola, branches down (a = −1< 0). Поэтому вершина будет точкой максимума:
x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2
The original function is exponential, it is monotonic, so the greatest value will be at the found point x 0 = −2:
An attentive reader will probably notice that we did not write out the range of permissible values of the root and logarithm. But this was not required: inside there are functions whose values are always positive.
Corollaries from the domain of a functionSometimes simply finding the vertex of the parabola is not enough to solve Problem B15. The value you are looking for may lie at the end of the segment, and not at all at the extremum point. If the problem does not indicate a segment at all, look at range of acceptable values original function. Namely:
Please note again: zero may well be under the root, but never in the logarithm or denominator of a fraction. Let's see how this works with specific examples:
Task. Find the largest value of the function:
Under the root is again a quadratic function: y = 3 − 2x − x 2 . Its graph is a parabola, but branches down because a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический Square root of a negative number does not exist.
We write out the range of permissible values (APV):
3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]
Now let's find the vertex of the parabola:
x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1
The point x 0 = −1 belongs to the ODZ segment - and this is good. Now we calculate the value of the function at the point x 0, as well as at the ends of the ODZ:
y(−3) = y(1) = 0
So, we got the numbers 2 and 0. We are asked to find the largest - this is the number 2.
Task. Find the smallest value of the function:
y = log 0.5 (6x − x 2 − 5)
Inside the logarithm there is a quadratic function y = 6x − x 2 − 5. This is a parabola with branches down, but there cannot be negative numbers in the logarithm, so we write out the ODZ:
6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)
Please note: the inequality is strict, so the ends do not belong to the ODZ. This differs the logarithm from the root, where the ends of the segment suit us quite well.
We are looking for the vertex of the parabola:
x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3
The vertex of the parabola fits according to the ODZ: x 0 = 3 ∈ (1; 5). But since we are not interested in the ends of the segment, we calculate the value of the function only at the point x 0:
y min = y (3) = log 0.5 (6 3 − 3 2 − 5) = log 0.5 (18 − 9 − 5) = log 0.5 4 = −2
In practice, it is quite common to use the derivative in order to calculate the largest and smallest value of a function. We perform this action when we figure out how to minimize costs, increase profits, calculate the optimal load on production, etc., that is, in cases where we need to determine the optimal value of a parameter. To solve such problems correctly, you need to have a good understanding of what the largest and smallest values of a function are.
Typically we define these values within a certain interval x, which in turn may correspond to the entire domain of the function or part of it. It can be like a segment [a; b ] , and open interval (a ; b) , (a ; b ] , [ a ; b) , infinite interval (a ; b) , (a ; b ] , [ a ; b) or infinite span- ∞ ; a , (- ∞ ; a ] , [ a ; + ∞) , (- ∞ ; + ∞) .
In this article we will tell you how to calculate the largest and smallest value explicitly given function with one variable y=f(x) y = f (x) .
Basic definitionsLet's start, as always, with the formulation of basic definitions.
Definition 1
The largest value of the function y = f (x) on a certain interval x is the value m a x y = f (x 0) x ∈ X, which for any value x x ∈ X, x ≠ x 0 makes the inequality f (x) ≤ f (x) valid 0) .
Definition 2
The smallest value of the function y = f (x) on a certain interval x is the value m i n x ∈ X y = f (x 0) , which for any value x ∈ X, x ≠ x 0 makes the inequality f(X f (x) ≥ f (x 0) .
These definitions are quite obvious. Even simpler, we can say this: the largest value of a function is its largest value on a known interval at abscissa x 0, and the smallest is the smallest accepted value on the same interval at x 0.
Definition 3
Stationary points are those values of the argument of a function at which its derivative becomes 0.
Why do we need to know what stationary points are? To answer this question, we need to remember Fermat's theorem. It follows from it that a stationary point is the point at which the extremum of the differentiable function is located (i.e., its local minimum or maximum). Consequently, the function will take the smallest or largest value on a certain interval precisely at one of the stationary points.
A function can also take on the largest or smallest value at those points at which the function itself is defined and its first derivative does not exist.
The first question that arises when studying this topic: in all cases can we determine the largest or smallest value of a function on a given interval? No, we cannot do this when the boundaries of a given interval coincide with the boundaries of the definition area, or if we are dealing with an infinite interval. It also happens that a function in a given segment or at infinity will take infinitely small or infinitely large values. In these cases, it is not possible to determine the largest and/or smallest value.
These points will become clearer after being depicted on the graphs:
The first figure shows us a function that takes the largest and smallest values (m a x y and m i n y) at stationary points located on the segment [ - 6 ; 6].
Let us examine in detail the case indicated in the second graph. Let's change the value of the segment to [ 1 ; 6 ] and we find that the maximum value of the function will be achieved at the point with the abscissa at the right boundary of the interval, and the minimum - at the stationary point.
In the third figure, the abscissas of the points represent the boundary points of the segment [ - 3 ; 2]. They correspond to the largest and smallest value of a given function.

Now let's look at the fourth picture. In it, the function takes m a x y (the largest value) and m i n y (the smallest value) at stationary points on the open interval (- 6; 6).
If we take the interval [ 1 ; 6), then we can say that the smallest value of the function on it will be achieved at a stationary point. The greatest value will be unknown to us. The function could take its maximum value at x equal to 6 if x = 6 belonged to the interval. This is exactly the case shown in graph 5.
On graph 6 the lowest value this function acquires at the right boundary of the interval (- 3; 2 ], and we cannot draw definite conclusions about the greatest value.

In Figure 7 we see that the function will have m a x y at a stationary point having an abscissa equal to 1. The function will reach its minimum value at the boundary of the interval on the right side. At minus infinity, the function values will asymptotically approach y = 3.
If we take the interval x ∈ 2 ; + ∞ , then we will see that the given function will take neither the smallest nor the largest value on it. If x tends to 2, then the values of the function will tend to minus infinity, since the straight line x = 2 is a vertical asymptote. If the abscissa tends to plus infinity, then the function values will asymptotically approach y = 3. This is exactly the case shown in Figure 8.
In this paragraph we will present the sequence of actions that need to be performed to find the largest or smallest value of a function on a certain segment.
Let's see how to correctly apply this algorithm when solving problems.
Example 1
Condition: the function y = x 3 + 4 x 2 is given. Determine its largest and smallest values on the segments [ 1 ; 4 ] and [ - 4 ; - 1 ] .
Solution:
Let's start by finding the domain of definition of a given function. In this case, she will have a lot of everyone real numbers, except 0 . In other words, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; + ∞ . Both segments specified in the condition will be inside the definition area.
Now we calculate the derivative of the function according to the rule of fraction differentiation:
y " = x 3 + 4 x 2 " = x 3 + 4 " x 2 - x 3 + 4 x 2 " x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x 3
We learned that the derivative of a function will exist at all points of the segments [ 1 ; 4 ] and [ - 4 ; - 1 ] .
Now we need to determine the stationary points of the function. Let's do this using the equation x 3 - 8 x 3 = 0. It has only one real root, which is 2. It will be a stationary point of the function and will fall into the first segment [1; 4 ] .
Let us calculate the values of the function at the ends of the first segment and at this point, i.e. for x = 1, x = 2 and x = 4:
y (1) = 1 3 + 4 1 2 = 5 y (2) = 2 3 + 4 2 2 = 3 y (4) = 4 3 + 4 4 2 = 4 1 4
We found that the largest value of the function m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 will be achieved at x = 1, and the smallest m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – at x = 2.
The second segment does not include a single stationary point, so we need to calculate the function values only at the ends of the given segment:
y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3
This means m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .
Answer: For the segment [ 1 ; 4 ] - m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 , for the segment [ - 4 ; - 1 ] - m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .
See picture:

Before studying this method, we advise you to review how to correctly calculate the one-sided limit and the limit at infinity, as well as learn the basic methods for finding them. To find the largest and/or smallest value of a function on an open or infinite interval, perform the following steps sequentially.
- If the interval is of the form [ a ; b) , then we need to calculate the value of the function at the point x = a and the one-sided limit lim x → b - 0 f (x) .
- If the interval has the form (a; b ], then we need to calculate the value of the function at the point x = b and the one-sided limit lim x → a + 0 f (x).
- If the interval has the form (a; b), then we need to calculate the one-sided limits lim x → b - 0 f (x), lim x → a + 0 f (x).
- If the interval is of the form [ a ; + ∞), then we need to calculate the value at the point x = a and the limit at plus infinity lim x → + ∞ f (x) .
- If the interval looks like (- ∞ ; b ] , we calculate the value at the point x = b and the limit at minus infinity lim x → - ∞ f (x) .
- If - ∞ ; b , then we consider the one-sided limit lim x → b - 0 f (x) and the limit at minus infinity lim x → - ∞ f (x)
- If - ∞; + ∞ , then we consider the limits on minus and plus infinity lim x → + ∞ f (x) , lim x → - ∞ f (x) .
Condition: given function y = 3 e 1 x 2 + x - 6 - 4 . Calculate its largest and smallest value in the intervals - ∞ ; - 4, - ∞; - 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞ , [ 4 ; + ∞) .
Solution
First of all, we find the domain of definition of the function. The denominator of the fraction contains a quadratic trinomial, which should not turn to 0:
x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)
We have obtained the domain of definition of the function to which all the intervals specified in the condition belong.
Now let's differentiate the function and get:
y" = 3 e 1 x 2 + x - 6 - 4 " = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " = = 3 · e 1 x 2 + x - 6 · 1 " · x 2 + x - 6 - 1 · x 2 + x - 6 " (x 2 + x - 6) 2 = - 3 · (2 x + 1) · e 1 x 2 + x - 6 x 2 + x - 6 2
Consequently, derivatives of a function exist throughout its entire domain of definition.
Let's move on to finding stationary points. The derivative of the function becomes 0 at x = - 1 2 . This is a stationary point that lies in the intervals (- 3 ; 1 ] and (- 3 ; 2) .
Let's calculate the value of the function at x = - 4 for the interval (- ∞ ; - 4 ], as well as the limit at minus infinity:
y (- 4) = 3 e 1 (- 4) 2 + (- 4) - 6 - 4 = 3 e 1 6 - 4 ≈ - 0 . 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1
Since 3 e 1 6 - 4 > - 1, it means that m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4. This does not allow us to uniquely determine the smallest value of the function. We can only conclude that there is a constraint below - 1, since it is to this value that the function approaches asymptotically at minus infinity.
The peculiarity of the second interval is that there is not a single stationary point and not a single strict boundary in it. Consequently, we will not be able to calculate either the largest or smallest value of the function. Having defined the limit at minus infinity and as the argument tends to - 3 on the left side, we get only an interval of values:
lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1
This means that the function values will be located in the interval - 1; +∞
To find the greatest value of the function in the third interval, we determine its value at the stationary point x = - 1 2 if x = 1. We will also need to know the one-sided limit for the case when the argument tends to - 3 on the right side:
y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1 . 444 y (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4
It turned out that the function will take the greatest value at a stationary point m a x y x ∈ (3; 1 ] = y - 1 2 = 3 e - 4 25 - 4. As for the smallest value, we cannot determine it. Everything we know , is the presence of a lower limit to - 4 .
For the interval (- 3 ; 2), take the results of the previous calculation and once again calculate what the one-sided limit is equal to when tending to 2 on the left side:
y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1 . 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 · 0 - 4 = - 4
This means that m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4, and the smallest value cannot be determined, and the values of the function are limited from below by the number - 4.
Based on what we got in the two previous calculations, we can say that on the interval [ 1 ; 2) the function will take the largest value at x = 1, but it is impossible to find the smallest.
On the interval (2 ; + ∞) the function will not reach either the largest or the smallest value, i.e. it will take values from the interval - 1 ; + ∞ .
lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1
Having calculated what the value of the function will be equal to at x = 4, we find out that m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 , and the given function at plus infinity will asymptotically approach the straight line y = - 1 .
Let's compare what we got in each calculation with the graph of the given function. In the figure, the asymptotes are shown by dotted lines.

That's all we wanted to tell you about finding the largest and smallest values of a function. The sequences of actions that we have given will help you make the necessary calculations as quickly and simply as possible. But remember that it is often useful to first find out at which intervals the function will decrease and at which it will increase, after which you can draw further conclusions. This way you can more accurately determine the largest and smallest values of the function and justify the results obtained.
If you notice an error in the text, please highlight it and press Ctrl+Enter

 Entrance
Entrance