EntranceOblique asymptote y x. Asymptotes
How many asymptotes can the graph of a function have?Not one, one, two, three,... or infinitely many. We won’t go far for examples, let’s remember elementary functions. A parabola, a cubic parabola, and a sine wave do not have asymptotes at all. The graph of an exponential, logarithmic function has a single asymptote. The arctangent and arccotangent have two of them, and the tangent and cotangent have infinitely many. It is not uncommon for a graph to have both horizontal and vertical asymptotes. Hyperbole, will always love you.
What does it mean to find the asymptotes of the graph of a function?
This means figuring out their equations, and drawing straight lines if the problem requires it. The process involves finding the limits of a function.
Vertical asymptotes of the graph of a functionThe vertical asymptote of the graph, as a rule, is located at the point of infinite discontinuity of the function. It’s simple: if a function has an infinite discontinuity at a point, then the straight line given by the equation is the vertical asymptote of the graph.
Note: Please note that the entry is used to refer to two completely different concepts. Whether a point is implied or an equation of a line depends on the context.
Thus, to establish the presence of a vertical asymptote at a point, it is enough to show that at least one of the one-sided limits is infinite. Most often this is the point where the denominator of the function is zero. Essentially, we have already found vertical asymptotes in the last examples of the lesson on continuity of a function. But in some cases there is only one one-sided limit, and if it is infinite, then again - love and favor the vertical asymptote. The simplest illustration: and the ordinate axis.
From the above, an obvious fact also follows: if the function is continuous on, then there are no vertical asymptotes. For some reason a parabola came to mind. Really, where can you “stick” a straight line here? ...yes... I understand... Uncle Freud's followers became hysterical =)
The converse statement is generally false: for example, the function is not defined on the entire number line, but is completely deprived of asymptotes.
Sloping asymptotes of the graph of a function
Oblique (as a special case - horizontal) asymptotes can be drawn if the argument of the function tends to “plus infinity” or to “minus infinity”. Therefore, the graph of a function cannot have more than 2 inclined asymptotes. For example, the graph of an exponential function has a single horizontal asymptote at, and the graph of the arctangent at has two such asymptotes, and different ones at that.
When the graph in both places approaches a single oblique asymptote, then it is customary to combine the “infinities” under a single entry. For example, ...you guessed correctly: .
One of the important stages of constructing function graphs is the search for asymptotes. We have encountered asymptotes more than once: when constructing graphs of functions, y=tgx, y=сtgx. We defined them as lines that the graph of a function “tends” to, but never crosses. The time has come to give a precise definition of asymptotes.
There are three types of asymptotes: vertical, horizontal and oblique. In the drawing, asymptotes are usually denoted by dotted lines.
Let's consider the following artificially constructed graph of the function (Fig. 16.1), in which all types of asymptotes are clearly visible:
Let us define each type of asymptote:
1. Direct x=a called vertical asymptote functions if .
2. Direct y=c called horizontal asymptote functions if .
3. Direct y=kx+b called oblique asymptote functions if .
Geometrically, the definition of an oblique asymptote means that at →∞ the graph of the function approaches a straight line as close as desired y=kx+b, i.e. they are almost identical. The difference between practically identical expressions tends to zero.
Note that horizontal and oblique asymptotes are considered only under the condition →∞. Sometimes they are distinguished into horizontal and oblique asymptotes at →+∞ and →-∞.
To find asymptotes, you can use the following algorithm:
There may be one, several or no vertical asymptotes.
- If c is a number, then y=c– horizontal asymptote;
- If c is infinity, then there are no horizontal asymptotes.
If a function is a ratio of two polynomials, then if the function has horizontal asymptotes, we will not look for oblique asymptotes - they do not exist.
Let's look at examples of finding asymptotes of a function:
Example 16.1. Find the asymptotes of the curve.
Solution X-1≠0; X≠1.
Let's check if the line is straight x= 1 vertical asymptote. To do this, we calculate the limit of the function at the point x= 1: .
x= 1 - vertical asymptote.
With= .
With= = . Because With=2 (number), then y=2– horizontal asymptote.
Since a function is a ratio of polynomials, if there are horizontal asymptotes, we assert that there are no oblique asymptotes.
x= 1 and horizontal asymptote y=2. For clarity, the graph of this function is presented in Fig. 16.2.
Example 16.2. Find the asymptotes of the curve.
Solution. 1. Find the domain of definition of the function: X-2≠0; X≠2.
Let's check if the line is straight x= 2 vertical asymptote. To do this, we calculate the limit of the function at the point x= 2: .
We got that, therefore, x= 2 - vertical asymptote.
2. To search for horizontal asymptotes, we find: With= .
Since uncertainty appears in the limit, we use L'Hopital's rule: With= = . Because With– infinity, then there are no horizontal asymptotes.
3. To search for oblique asymptotes, we find:
We have obtained an uncertainty of the form , let's use L'Hopital's rule: = =1. So, 1. Let's find b according to the formula: .
b= = =
Got that b= 2. Then y=kx+b – oblique asymptote. In our case it looks like: y=x+2.
|
Lecture 17. GENERAL SCHEME FOR STUDYING A FUNCTION AND CONSTRUCTING A GRAPH
In this lecture we will summarize all the previously studied material. The ultimate goal of our long journey is to be able to investigate any analytically. given function and build its schedule. Important links Our research will examine the function for extrema, determine the intervals of monotonicity, convexity and concavity of the graph, search for inflection points, asymptotes of the graph of the function.
Taking into account all the above aspects, we present scheme for studying a function and plotting a graph .
1. Find the domain of definition of the function.
2. Examine the function for even-odd parity:
· if , then the function is even (the graph of an even function is symmetrical about the axis Oh);
· if , then the function is odd (the graph of an odd function is symmetrical with respect to the origin);
· otherwise the function is neither even nor odd.
3. Investigate the function for periodicity (among the functions we study, only trigonometric functions can be periodic).
4. Find the points of intersection of the function graph with the coordinate axes:
· Oh: at=0 (we solve the equation only if we can use methods known to us);
· Oh: X=0.
5. Find the first derivative of the function and critical points of the first kind.
6. Find monotonicity intervals and extrema of the function.
7. Find the second derivative of the function and critical points of the second kind.
8. Find the convexity-concavity intervals of the function graph and inflection points.
9. Find the asymptotes of the graph of the function.
10. Construct a graph of the function. When constructing, you should take into account cases of possible location of the graph near asymptotes :
11. If necessary, select control points for more accurate construction.
Let's consider a scheme for studying a function and constructing its graph on specific examples:
Example 17.1. Graph the function.
Solution. 1. This function is defined on the entire number line except X=3, because at this point the denominator goes to zero.
2. To determine whether a function is even or odd, we find:
We see that and , therefore, is neither an even nor an odd function.
3. The function is non-periodic.
4. Find the points of intersection with the coordinate axes. To find the point of intersection with the axis Oh let's accept at=0. We get the equation: . So, point (0; 0) is the point of intersection with the coordinate axes.
5. Let's find the derivative of the function using the rule of differentiation of fractions: = = = = .
To find critical points, we find the points at which the derivative of the function is equal to 0 or does not exist.
If =0, therefore . The product is then equal to 0 when at least one of the factors is equal to 0: or .
X-3) 2 is equal to 0, i.e. does not exist when X=3.
So, the function has three critical points of the first kind: ; ; .
6. On the numerical axis we mark critical points of the first kind, and we mark the point with a punctured dot, because the function is not defined in it.
We place the derivative = signs on each interval:
|
|
On intervals where , the original function increases (at (-∞;0]), where - decreases (at ).
Dot X=0 is the maximum point of the function. To find the maximum of the function, we find the value of the function at point 0: .
Dot X=6 is the minimum point of the function. To find the minimum of the function, we find the value of the function at point 6: .
The research results can be entered into a table. The number of rows in the table is fixed and equal to four, and the number of columns depends on the function being studied. In the cells of the first line, intervals are sequentially entered into which the critical points divide the domain of definition of the function, including the critical points themselves. To avoid errors when constructing points that do not belong to the definition domain, you can not include them in the table.
The second line of the table displays the signs of the derivative at each of the intervals under consideration and the value of the derivative at critical points. In accordance with the signs of the derivative of the function, the intervals of increase, decrease, and extrema of the function are marked in the third line.
The last line serves to indicate the maximum and minimum of the function.
| X | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f(x) | |||||||
| Conclusions | max | min |
7. Let’s find the second derivative of the function as the derivative of the first derivative: = =
Let's put it in the numerator X-3 for brackets and perform the reduction:
Let us present similar terms in the numerator: .
Let's find critical points of the second kind: points at which the second derivative of the function is equal to zero or does not exist.
0 if =0. This fraction cannot equal zero, therefore, there are no points at which the second derivative of the function equals zero.
Does not exist if denominator ( X-3) 3 is equal to 0, i.e. does not exist when X=3. :Oh , Oh, origin, units of measurement for each axis.
Before plotting a function, you need to:
Draw the asymptotes with dotted lines;
· mark the points of intersection with the coordinate axes;
|
· using the obtained data on the intervals of increase, decrease, convexity and concavity, construct a graph of the function. The branches of the graph should “tend” to asymptotes, but not intersect them.
· check whether the graph of the function corresponds to the research conducted: if the function is even or odd, then whether symmetry is observed; Do the intervals of increase and decrease, convexity and concavity, and inflection points correspond to the theoretically found ones?
11. For more accurate construction, you can select several control points. For example, let's find the values functions at points -2 and 7:
We adjust the schedule taking into account control points.
Security questions:
CHAPTER 3. 3. INTEGRAL CALCULUS OF A FUNCTION
In July 2020, NASA launches an expedition to Mars. Spacecraft will deliver to Mars an electronic medium with the names of all registered expedition participants.
Registration of participants is open. Get your ticket to Mars using this link.
If this post solved your problem or you just liked it, share the link to it with your friends on social networks.
One of these code options needs to be copied and pasted into the code of your web page, preferably between tags and or immediately after the tag. According to the first option, MathJax loads faster and slows down the page less. But the second option automatically monitors and loads the latest versions of MathJax. If you insert the first code, it will need to be updated periodically. If you insert the second code, the pages will load more slowly, but you will not need to constantly monitor MathJax updates.
The easiest way to connect MathJax is in Blogger or WordPress: in the site control panel, add a widget designed to insert third-party JavaScript code, copy the first or second version of the download code presented above into it, and place the widget closer to the beginning of the template (by the way, this is not at all necessary , since the MathJax script is loaded asynchronously). That's it. Now learn the markup syntax of MathML, LaTeX and ASCIIMathML and you are ready to embed mathematical formulas to the web pages of your site.
Another New Year's Eve... frosty weather and snowflakes on the window glass... All this prompted me to write again about... fractals, and what Wolfram Alpha knows about it. There is an interesting article on this subject, which contains examples of two-dimensional fractal structures. Here we will look at more complex examples three-dimensional fractals.
A fractal can be visually represented (described) as a geometric figure or body (meaning that both are a set, in this case, a set of points), the details of which have the same shape as the original figure itself. That is, this is a self-similar structure, examining the details of which when magnified, we will see the same shape as without magnification. Whereas in the case of ordinary geometric figure(not a fractal), when zoomed in we will see details that have a simpler shape than the original figure itself. For example, at a high enough magnification, part of an ellipse looks like a straight line segment. This does not happen with fractals: with any increase in them, we will again see the same complex shape, which will be repeated again and again with each increase.
Benoit Mandelbrot, the founder of the science of fractals, wrote in his article Fractals and Art in the Name of Science: “Fractals are geometric shapes that are as complex in their details as they are in their general form. That is, if part of a fractal is enlarged to the size of the whole, it will appear as the whole, either exactly, or perhaps with a slight deformation."
If you first construct the asymptotes of the curve, then in many cases the construction of a graph of the function becomes easier.
The fate of the asymptote is full of tragedy. Imagine what it’s like: all your life moving in a straight line towards your cherished goal, getting as close as possible to it, but never achieving it. For example, strive to connect your life path with the path of the desired person, at some point approach him almost closely, but not even touch him. Or strive to earn a billion, but before achieving this goal and entering the Guinness Book of Records for your case, hundredths of a cent are missing. And the like. So it is with an asymptote: it constantly strives to reach the curve of the function graph, approaches it to the minimum possible distance, but never touches it.
Definition 1. Asymptotes are those straight lines to which the graph of a function approaches arbitrarily closely when the variable tends to plus infinity or minus infinity.
Definition 2. A straight line is called an asymptote of the graph of a function if the distance from the variable point M the graph of the function up to this line tends to zero as the point moves away indefinitely M from the origin along any branch of the function graph.
There are three types of asymptotes: vertical, horizontal and oblique.
Vertical asymptotesThe first thing you need to know about vertical asymptotes is that they are parallel to the axis Oy .
Definition . Straight x = a is vertical asymptote of the graph of the function, if point x = a is a discontinuity point of the second kind for this function.
From the definition it follows that the straight line x = a is the vertical asymptote of the graph of the function f(x) if at least one of the conditions is met:
In this case, the function f(x) may not be defined at all, respectively, when x ≥ a And x ≤ a .
Comment:
Example 1. Graph of a function y=ln x has a vertical asymptote x= 0 (i.e. coinciding with the axis Oy) on the boundary of the domain of definition, since the limit of the function as x tends to zero from the right is equal to minus infinity:
(picture above).
yourself and then see the solutionsExample 2. Find asymptotes of the graph of the function.
Example 3. Find asymptotes of the graph of a function
Horizontal asymptotesThe first thing you need to know about horizontal asymptotes is that they are parallel to the axis Ox .
If (the limit of a function as the argument tends to plus or minus infinity is equal to a certain value b), That y = b – horizontal asymptote crooked y = f(x) (right when X tends to plus infinity, left when X tends to minus infinity, and two-sided if the limits as X tends to plus or minus infinity are equal).
Example 5. Graph of a function
at a> 1 has left horizontal asympotote y= 0 (i.e. coinciding with the axis Ox), since the limit of the function as “x” tends to minus infinity is zero:
The curve does not have a right horizontal asymptote, since the limit of the function as “x” tends to plus infinity is equal to infinity:
Oblique asymptotesVertical and horizontal asymptotes, which we examined above, are parallel to the coordinate axes, so to construct them we only needed a certain number - a point on the abscissa or ordinate axis through which the asymptote passes. For an oblique asymptote, a larger slope is needed k, which shows the angle of inclination of the line, and the free term b, which shows how much the line is above or below the origin. Those who have not forgotten analytical geometry, and from it the equations of a straight line, will notice that for an oblique asymptote they find an equation of a straight line with an angular coefficient. The existence of an oblique asymptote is determined by the following theorem, on the basis of which the coefficients just mentioned are found.
Theorem. To make the curve y = f(x) had an asymptote y = kx + b, necessary and sufficient for them to exist finite limits k And b of the function under consideration as the variable tends x to plus infinity and minus infinity:
(1)
(2)
The numbers found in this way k And b and are the oblique asymptote coefficients.
In the first case (as x tends to plus infinity), a right inclined asymptote is obtained, in the second (as x tends to minus infinity), a left oblique asymptote is obtained. The right oblique asymptote is shown in Fig. below.
When finding the equation for an oblique asymptote, it is necessary to take into account the tendency of X to both plus infinity and minus infinity. For some functions, for example, fractional rational ones, these limits coincide, but for many functions these limits are different and only one of them can exist.
If the limits coincide and x tends to plus infinity and minus infinity, the straight line y = kx + b is the two-sided asymptote of the curve.
If at least one of the limits defining the asymptote y = kx + b, does not exist, then the graph of the function does not have an oblique asymptote (but may have a vertical one).
It is easy to see that the horizontal asymptote y = b is a special case of oblique y = kx + b at k = 0 .
Therefore, if in any direction a curve has a horizontal asymptote, then in this direction there is no inclined one, and vice versa.
Example 6. Find asymptotes of the graph of a function
Solution. The function is defined on the entire number line except x= 0, i.e.
Therefore, at the breaking point x= 0 the curve may have a vertical asymptote. Indeed, the limit of the function as x tends to zero from the left is equal to plus infinity:
Hence, x= 0 – vertical asymptote of the graph of this function.
The graph of this function does not have a horizontal asymptote, since the limit of the function as x tends to plus infinity is equal to plus infinity:
Let us find out the presence of an oblique asymptote:
Got finite limits k= 2 and b= 0 . Straight y = 2x is the two-way slanted asymptote of the graph of this function (figure inside the example).
Example 7. Find asymptotes of the graph of a function
Solution. The function has one breakpoint x= −1 . Let's calculate one-sided limits and determine the type of discontinuity:
Conclusion: x= −1 is a discontinuity point of the second kind, so the straight line x= −1 is the vertical asymptote of the graph of this function.
We are looking for oblique asymptotes. Since this function is fractional-rational, the limits at and at will coincide. Thus, we find the coefficients for substituting the straight line - oblique asymptote into the equation:
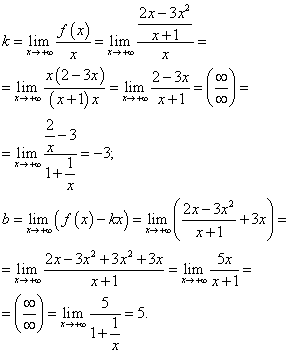
Substituting the found coefficients into the equation of the straight line with the slope coefficient, we obtain the equation of the oblique asymptote:
y = −3x + 5 .
In the figure, the graph of the function is indicated in burgundy, and the asymptotes are indicated in black.
Example 8. Find asymptotes of the graph of a function
Solution. Since this function is continuous, its graph has no vertical asymptotes. We are looking for oblique asymptotes:
.
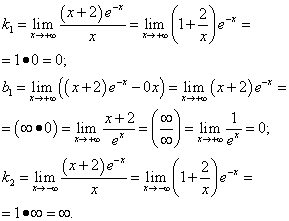Thus, the graph of this function has an asymptote y= 0 at and has no asyptote at .
Example 9. Find asymptotes of the graph of a function
Solution. First we look for vertical asymptotes. To do this, we find the domain of definition of the function. A function is defined when the inequality and . Sign of the variable x matches the sign. Therefore, consider the equivalent inequality. From this we obtain the domain of definition of the function: 
. A vertical asymptote can only be on the boundary of the domain of definition of the function. But x= 0 cannot be a vertical asymptote, since the function is defined at x = 0
.
Consider the right-hand limit at (there is no left-hand limit):
.
Dot x= 2 is a discontinuity point of the second kind, so the straight line x= 2 - vertical asymptote of the graph of this function.
We are looking for oblique asymptotes:
So, y = x+ 1 - oblique asymptote of the graph of this function at . We are looking for an oblique asymptote at:
So, y = −x− 1 - oblique asymptote at .
Example 10. Find asymptotes of the graph of a function
Solution. A function has a domain of definition 
. Since the vertical asymptote of the graph of this function can only be on the boundary of the domain of definition, we find the one-sided limits of the function at .
Definition. An asymptote of the graph of a function is a straight line that has the property that the distance from a point on the graph of a function to this straight line tends to zero as the graph point moves indefinitely from the origin..
According to the methods of finding them, three types of asymptotes are distinguished: vertical, horizontal, oblique.
Obviously, horizontal ones are special cases of inclined ones (at ).
Finding the asymptotes of the graph of a function is based on the following statements.
Theorem 1. Let the function be defined at least in some semi-neighborhood of a point and at least one of its one-sided limits at this point is infinite, i.e. equalized. Then the straight line is the vertical asymptote of the graph of the function.
Thus, vertical asymptotes of the graph of a function should be sought at the discontinuity points of the function or at the ends of its domain of definition (if these are finite numbers).
Theorem 2.
Let the function be defined for argument values sufficiently large in absolute value, and there is a finite limit of the function 
. Then the straight line is the horizontal asymptote of the graph of the function.
It may happen that 
, A 
, and are finite numbers, then the graph has two different horizontal asymptotes: left-handed and right-handed. If only one of the finite limits or exists, then the graph has either one left-handed or one right-handed horizontal asymptote.
Theorem 3.
Let the function be defined for values of the argument that are sufficiently large in absolute value, and there are finite limits 
And 
. Then the straight line is the slanted asymptote of the graph of the function.
Note that if at least one of these limits is infinite, then there is no oblique asymptote.
An oblique asymptote, like a horizontal one, can be one-sided.
Example. Find all asymptotes of the graph of the function.
Solution .
The function is defined at . Let us find its one-sided limits at points.
Because 
And 
(the other two one-sided limits may no longer be found), then the straight lines are vertical asymptotes of the graph of the function.
Let's calculate
(apply L'Hopital's rule) = 
.
This means that the straight line is a horizontal asymptote.
Since the horizontal asymptote exists, we are no longer looking for inclined ones (they don’t exist).
Answer: The graph has two vertical asymptotes and one horizontal.
General function research y = f(x).
The scope of the function. Find its domain of definition D(f) . If it's not too difficult, it's useful to also find the range E(f) . (However, in many cases, the question of finding E(f) is postponed until the extrema of the function are found.)
Special properties of the function. Find out general properties functions: even, odd, periodicity, etc. Not every function has properties such as even or odd. A function is obviously neither even nor odd if its domain of definition is asymmetrical with respect to point 0 on the axis Ox. In the same way, for any periodic function the domain of definition consists either of the entire real axis or of the union of periodically repeating systems of intervals.
Vertical asymptotes. Find out how the function behaves when the argument approaches the boundary points of the domain of definition D(f), if such boundary points exist. In this case, vertical asymptotes may appear. If a function has discontinuity points at which it is not defined, then these points should also be checked for the presence of vertical asymptotes of the function.
Oblique and horizontal asymptotes. If the domain of definition D(f) includes rays of the form (a;+) or (−;b), then you can try to find oblique asymptotes (or horizontal asymptotes) for x+ or x−, respectively, i.e. find limxf(x). Oblique asymptotes: y = kx + b, where k=limx+xf(x) and b=limx+(f(x)−x). Asymptotes are horizontal: y = b, where limxf(x)=b.
Finding the intersection points of the graph with the axes. Finding the intersection point of the graph with the axis Oy. To do this you need to calculate the value f(0). Find also the points of intersection of the graph with the axis Ox, why find the roots of the equation f(x) = 0 (or make sure there are no roots). The equation can often be solved only approximately, but separating the roots helps to better understand the structure of the graph. Next, you need to determine the sign of the function on the intervals between the roots and break points.
Finding the intersection points of the graph with the asymptote. In some cases, it may be necessary to find characteristic points of the graph that were not mentioned in the previous paragraphs. For example, if a function has a slanted asymptote, then you can try to find out if the graph has intersection points with this asymptote.
Finding intervals of convexity and concavity. This is done by examining the sign of the second derivative f(x). Find inflection points at the junctions of the convex and concave intervals. Calculate the value of the function at the inflection points. If a function has other points of continuity (except for inflection points) at which the second derivative is 0 or does not exist, then it is also useful to calculate the value of the function at these points. Having found f(x) we solve the inequality f(x)0. On each of the solution intervals the function will be convex downwards. By solving the inverse inequality f(x)0, we find the intervals on which the function is convex upward (that is, concave). We define inflection points as those points at which the function changes direction of convexity (and is continuous).