EntranceDerivatives of simple trigonometric functions. Derivation of derivatives of inverse trigonometric functions Derivatives of inverse trigonometric functions
Derivatives of inverses are presented trigonometric functions and derivation of their formulas. Expressions for higher order derivatives are also given. Links to pages with a more detailed description of the derivation of formulas.
ContentSee also: Inverse trigonometric functions, their graphs and formulas
First, we derive the formula for the derivative of the arcsine. Let
y = arcsin x.
Since arcsine is the inverse function of sine, then
.
Here y is a function of x. Differentiate with respect to the variable x:
.
We apply:
.
So we found:
.
Because , then . Then
.
And the previous formula takes the form:
. From here
.
In exactly this way, you can obtain the formula for the derivative of the arc cosine. However, it is easier to use a formula relating inverse trigonometric functions:
.
Then
.
A more detailed description is presented on the page “Derivation of the derivatives of arcsine and arccosine”. There it is given derivation of derivatives in two ways- discussed above and according to the formula for the derivative of the inverse function.
Derivation of derivatives of arctangent and arccotangent
In the same way we will find the derivatives of arctangent and arccotangent.
Let
y = arctan x.
Arctangent is the inverse function of tangent:
.
Differentiate with respect to the variable x:
.
We apply the formula for the derivative of a complex function:
.
So we found:
.
Derivative of arc cotangent:
.
Arcsine derivatives
Let
.
We have already found the first-order derivative of the arcsine:
.
By differentiating, we find the second-order derivative:
;
.
It can also be written in the following form:
.
From here we get differential equation, which is satisfied by the arcsine derivatives of the first and second orders:
.
By differentiating this equation, we can find higher order derivatives.
Derivative of arcsine of nth order
The derivative of the arcsine of the nth order has the following form:
,
where is a polynomial of degree . It is determined by the formulas:
;
.
Here .
The polynomial satisfies the differential equation:
.
Derivative of arccosine of nth order
Derivatives for the arc cosine are obtained from derivatives for the arc sine using the trigonometric formula:
.
Therefore, the derivatives of these functions differ only in sign:
.
Derivatives of arctangent
Let . We found the derivative of the arc cotangent of the first order:
.
Let's break down the fraction into its simplest form:
.
Here is the imaginary unit, .
We differentiate once and bring the fraction to a common denominator:
.
Substituting , we get:
.
Derivative of arctangent of nth order
Thus, the derivative of the arctangent of the nth order can be represented in several ways:
;
.
Derivatives of arc cotangent
Let it be now. Let us apply the formula connecting inverse trigonometric functions:
.
Then the nth order derivative of the arc tangent differs only in sign from the derivative of the arc tangent:
.
Substituting , we find:
.
References:
N.M. Gunter, R.O. Kuzmin, Collection of problems on higher mathematics, "Lan", 2003.
Page navigation.
The derivative is constant.
When deriving the very first formula of the table, we will proceed from the definition of the derivative of a function at a point. Let's take , where x is any real number, that is, x is any number from the domain of definition of the function. Let us write down the limit of the ratio of the increment of the function to the increment of the argument at : 
It should be noted that under the limit sign the expression is obtained, which is not , since the numerator does not contain an infinitesimal value, but precisely zero. In other words, the increment of a constant function is always zero.
Thus, the derivative of a constant function is equal to zero throughout the entire domain of definition.
Example.
Find derivatives of the following constant functions
Solution.
In the first case we have the derivative of the natural number 3, in the second case we have to take the derivative of the parameter a, which can be any real number, in the third - the derivative irrational number, in the fourth case we have the derivative of zero (zero is an integer), in the fifth case we have the derivative of a rational fraction.
Answer:
The derivatives of all these functions are equal to zero for any real x (over the entire domain of definition) 
Derivative of a power function.
Derivative formula power function looks like 
, where the exponent p is any real number.
Let us first prove the formula for the natural exponent, that is, for p = 1, 2, 3, ...
We will use the definition of derivative. Let us write down the limit of the ratio of the increment of a power function to the increment of the argument: 
To simplify the expression in the numerator, we turn to the formula: 
Hence, 
This proves the formula for the derivative of a power function for a natural exponent.
Two cases should be considered: for positive x and negative x.
Let's assume first. In this case . Let's take the logarithm of the equality to base e and apply the property of the logarithm:
We arrived at an implicitly specified function. We find its derivative: 
It remains to carry out the proof for negative x.
When the exponent p is an even number, then the power function is also defined for and is even (see section). That is, 
. In this case, you can also use the proof through the logarithmic derivative.
When the exponent p is an odd number, then the power function is also defined for and is odd. That is, 
. In this case, the logarithmic derivative cannot be used. To prove the formula in this case, you can use the rules of differentiation and the rule for finding the derivative of a complex function: 
The last transition is possible due to the fact that if p is an odd number, then p-1 is either an even number or zero (for p=1), therefore, for negative x the equality is true 
.
Thus, the formula for the derivative of a power function is proven for any real p.
Example.
Find derivatives of functions.
Solution.
We bring the first and third functions to tabular form, using the properties of a power, and apply the formula for the derivative of a power function: 
Derivative of an exponential function.
We present the derivation of the derivative formula based on the definition:
We have arrived at uncertainty. To expand it, we introduce a new variable, and at . Then . In the last transition, we used the formula for transitioning to a new logarithmic base.
Let's substitute into the original limit: 
By definition of the derivative for the sine function we have 
.
Let's use the difference of sines formula: 
It remains to turn to the first remarkable limit: 
Thus, the derivative functions sin x is cos x.
The formula for the derivative of the cosine is proved in exactly the same way. 
When solving differentiation problems, we will constantly refer to the table of derivatives of basic functions, otherwise why did we compile it and prove each formula. We recommend that you remember all these formulas; in the future it will save you a lot of time.
Copyright by cleverstudents
All rights reserved.
Protected by copyright law. No part of the site, including internal materials and appearance, may be reproduced in any form or used without the prior written permission of the copyright holder.
To find derivative of a trigonometric function need to use table of derivatives, namely derivatives 6-13.
When you find derivatives of simple trigonometric functions To avoid common mistakes, you should pay attention to the following points:
- in a function expression, one of the terms is often sine, cosine or other trigonometric function not from the argument of the function, but from the number (constant), therefore the derivative of this term is equal to zero;
- almost always you need to simplify the expression obtained as a result of differentiation, and for this you need to confidently use knowledge of operations with fractions;
- to simplify the expression you almost always need to know trigonometric identities, for example, the double angle formula and the unit formula as the sum of the squares of sine and cosine.
Example 1. Find the derivative of a function
Solution. Let's say with derivative of cosine everything is clear, many who begin to study derivatives will say. What about derivative of sine twelve divided by pi? Answer: consider it equal to zero! Here the sine (a function after all!) is a trap, because the argument is not the variable X or any other variable, but just a number. That is, the sine of this number is also a number. And the derivative of a number (constant), as we know from the table of derivatives, is equal to zero. So, we leave only the minus sine of X and find its derivative, not forgetting about the sign:
.
Example 2. Find the derivative of a function
.
Solution. The second term is the same case as the first term in the previous example. That is, it is a number, and the derivative of the number is zero. We find the derivative of the second term as the derivative of the quotient:
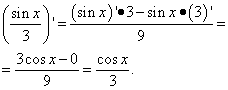
Example 3. Find the derivative of a function
Solution. This is another problem: here in the first term there is no arcsine or other trigonometic function, but there is x, which means it is a function of x. Therefore, we differentiate it as a term in the sum of functions:
Here skills in operations with fractions were required, namely, in eliminating the three-story structure of a fraction.
Example 4. Find the derivative of a function
.
Solution. Here the letter "phi" plays the same role as "x" in the previous cases (and in most others, but not all) - the independent variable. Therefore, when we look for the derivative of a product of functions, we will not rush to declare the derivative of the root of “phi” equal to zero. So:
But the solution doesn't end there. Since similar terms are collected in two brackets, we are still required to transform (simplify) the expression. Therefore, we multiply the brackets by the factors behind them, and then we bring the terms to a common denominator and perform other elementary transformations:
Example 5. Find the derivative of a function
Solution. In this example, we will need to know the fact that there is such a trigonometric function - the secant - and its formulas through the cosine. Let's differentiate:
Example 6. Find the derivative of a function
.
Solution. In this example, we will be required to remember the double angle formula from school. But first let's differentiate:
,
(this is the double angle formula)
II semester
- Signs of increasing and decreasing function. Lagrange's theorem.
Definition of an increasing function.
The function y = f(x) increases on the interval X if for any and 
inequality holds. In other words, a larger argument value corresponds to a larger function value.
Definition of a decreasing function.
The function y = f(x) decreases on the interval X if for any and 
inequality holds. In other words, a larger value of the argument corresponds to a smaller value of the function.
Lagrange's theorem: Let's use geometric sense derivative in order to give a visual explanation of the validity of the fact that there is a tangent to the graph f at the point with the abscissa c from the interval (a; b), parallel to the secant passing through the points A (a; f (a)), B (b; f ( b)).
Consider a straight line l, parallel to AB and having no common points with the part of the graph corresponding to the interval [a; b]. We will move this straight line l towards the graph f so that it remains parallel to AB. Let us fix the position l 0 of this line at the moment when it has common points with this part of the graph.
From Fig. 1 it is clear that any of these “first” common points is the point of tangency of the straight line l 0 with the graph f. Let us denote the abscissa of this point by c. Then f’(c)=tg α, where α is the angle between straight line l 0 and the abscissa axis. But l||AB, therefore the angle α is equal to the angle of inclination of the secant AB, i.e. So, if the function is differentiable, then on the interval (a; b) there is a point c∈ (a; b) (Fig. 2) such that 
- Sufficient sign decreasing function. If f'(x)< 0 в каждой точке интервала I, то функция f убывает на I.
Sufficient signs of increasing and decreasing functions:
- if the function f(x) at each point of the interval (a, b) has a positive derivative, then the function itself increases in this interval;
- if the function f(x) at each point of the interval (a,b) has a negative derivative, then the function decreases in this interval.
Definition. The function y=f(x) has an extremum (maximum or minimum) at the point x=x 0 if f(x 0) is the largest or lowest value functions in some neighborhood of this point.
- Extrema of a function. Study of a function for extrema in 1 derivative.
The function y=f(x) is said to be increasing (decreasing) in a certain interval if at x 1< x 2 выполняется неравенство f(x 1) < f (x 2) (f(x 1) >f(x 2)).
If the differentiable function y = f(x) increases (decreases) on an interval, then its derivative on this interval f ¢(x) > 0 (f ¢(x)< 0).
A point x 0 is called a local maximum (minimum) point of a function f(x) if there is a neighborhood of the point x 0 for which the inequality f(x) £ f(x 0) (f(x) ³ f(x 0) is true for all points ).
The maximum and minimum points are called extremum points, and the values of the function at these points are called its extrema.
Necessary conditions for an extremum. If the point xо is the extremum point of the function f(x), then either f ¢(x 0) = 0 or f ¢(x 0) does not exist. Such points are called critical, and the function itself is defined at the critical point. The extrema of a function should be sought among its critical points.
From the 1st derivative:
Let x 0 be the critical point. If f ¢ (x) changes sign from plus to minus when passing through point x 0, then at point x 0 the function has a maximum, otherwise it has a minimum. If the derivative does not change sign when passing through the critical point, then there is no extremum at point x0.
Necessary conditions for an extremum. If the point x 0 is the extremum point of the function f(x), then either f ¢(x 0) = 0 or f ¢(x 0) does not exist. Such points are called critical, and the function itself is defined at the critical point. The extrema of a function should be sought among its critical points.
- Convexity of the graph of a function. Inflection points.
Convexity of a function, inflection points
The chord connecting the points M 1 (x 1, f(x 1)), M 2 (x 2, f(x 2)) of the graph of the function f(x) is given by the function
y=L(x, x 1 , x 2) = f(x 1) + f(x 2) (*)
This is checked by substituting the coordinates x 1 , x 2 into the right side.
Definition. A function f(x) is said to be convex upward on , if for "x 1 L(x, x 1 , x 2) = f(x 1) If f is continuous on , twice differentiable on (a,b) and f¢¢(x)>0 on (a,b), then f is strictly downward convex. Proof. "a£x 1 Definition. A point x 0 is called an inflection point of a function f if there is a tangent at the point x 0 and in some neighborhood of the point x 0 the graph of f lies on opposite sides of the tangent. The greatest value of a function on an interval is the largest of all its values on this interval, and the smallest is the smallest of all its values. Consider the function y=f(x) continuous on the segment. As is known, such a function reaches its maximum and minimum values, either at the boundary of the segment or inside it. If the largest or smallest value of a function is achieved at an internal point of the segment, then this value is the maximum or minimum of the function, that is, it is achieved at critical points. Thus, we obtain the following rule for finding the largest and smallest values of a function on a segment: 1. Find all critical points of the function in the interval (a, b) and calculate the values of the function at these points. 2.Calculate the values of the function at the ends of the segment at x = a, x = b. 3.From all the obtained values, select the largest and smallest. 1 a.Find the ODZ and discontinuity points of the function. b.Find the points of intersection of the graph of the function with the coordinate axes. 2. Conduct a study of the function using the first derivative, that is, find the extremum points of the function and the intervals of increase and decrease. 3. Investigate the function using the second-order derivative, that is, find the inflection points of the function graph and the intervals of its convexity and concavity. 4. Find the asymptotes of the graph of the function: a) vertical, b) oblique. 5. Based on the research, construct a graph of the function. Definition. A function F (x) is called antiderivative for a function f (x) on a given interval if for any x from a given interval F"(x)= f (x). Example: 1. Find out whether the function F (x) = x 3 – 3x + 1 is antiderivative for the function f (x) = 3 (x 2 – 1). Solution: F"(x) = (x 3 – 3x + 1)′ = 3x 2 – 3 = 3(x 2 – 1) = f(x), i.e. F"(x) = f(x) , therefore, F(x) is an antiderivative of the function f(x). The set of antiderivatives of the function f(x) is called the indefinite integral of this function and is denoted by the symbol. As follows from the above, if F(x) is some antiderivative of the function f(x), then Properties of the indefinite integral that follow directly from the definition: Examples of flat figures General equation of a line
The general equation of a straight line on a plane in Cartesian coordinates is: where A, B and C are arbitrary constants, and the constants A and B are not equal to zero at the same time. A vector with coordinates (A,B) is called a normal vector and it is perpendicular to the line. The vector with coordinates (-B,A) or (B,-A) is called a direction vector. Equation of a line passing through two given non-coinciding points
Equation of a line passing through two given non-coinciding points and Parametric equations of a straight line.
Parametric equations of a straight line can be written as: Canonical equation of the line
The canonical equation is obtained from parametric equations by dividing one equation by another: Where are the X and Y coordinates of the direction vector of the line, and the coordinates of the point belonging to the line. General equation
Ax + By + C ( > 0).
Vector = (A; B) - normal vector straight. Special cases: 1) By + C = 0 - the straight line is parallel to the Ox axis; 2) Ax + C = 0 - straight line parallel to the Oy axis; 3) Ax + By = 0 - the straight line passes through the origin; 4) y = 0 - Ox axis; 5) x = 0 - Oy axis. Condition for parallel lines: k 1 = k 2. The condition for perpendicularity of lines: k 1 ·k 2 = −1. The angle between intersecting lines on a plane is the degree measure of the smallest of the angles formed at the intersection of these lines. The angle between coinciding or parallel lines is considered equal to zero. Angle α between two straight lines, given equations: y=k1x+b1 (first line) and y=k2x+b2 (second line), can be calculated by the formula (the angle is counted from the 1st line to the 2nd counterclockwise): tg(α)=(k2-k1)/(1+k1k2) Theorem. If a line that does not lie in a given plane is parallel to some line that lies in this plane, then it is parallel to the plane itself. a) the straight line lies in the plane; b) a straight line and a plane have only one common point; c) a straight line and a plane do not have a single common point. Definition. Two planes are called parallel if they have no common points. The parallelism of planes is denoted as follows: || . Let's consider the sign of parallelism of two planes. Theorem. If two intersecting lines of one plane are respectively parallel to two lines of another plane, then these planes are parallel. Properties of parallel planes: Segments of parallel lines enclosed between parallel planes, are equal. Signs of parallelism between a straight line and a plane: 1) If a line lying outside the plane is parallel to any line lying in this plane, then it is parallel to this plane. 2) If a line and a plane are perpendicular to the same line, then they are parallel. Signs of parallel planes: 1) If two intersecting lines of one plane are respectively parallel to two intersecting lines of another plane, then these planes are parallel. 2) If two planes are perpendicular to the same line, then they are parallel. Signs of perpendicularity of a straight line and a plane: 1) If a line is perpendicular to two intersecting lines lying in a plane, then it is perpendicular to this plane. 2) If a plane is perpendicular to one of the parallel lines, then it is also perpendicular to the other. Inclined to the plane. A straight line that intersects a plane and is not perpendicular to it is called inclined to the plane. Theorem of three perpendiculars. A straight line lying in a plane and perpendicular to the projection of an inclined one to this plane is also perpendicular to the inclined one. Signs of parallel lines in space: 1) If two lines are perpendicular to the same plane, then they are parallel. 2) If in one of the intersecting planes there is a straight line parallel to the other plane, then it is parallel to the line of intersection of the planes. A sign of perpendicularity of planes: if a plane passes through a line perpendicular to another plane, then these planes are perpendicular. Theorem on the common perpendicular to two skew lines. For any two skew lines there is a unique common perpendicular. THEOREM ABOUT THREE PERPENDICULARS. If a straight line drawn on a plane through the base of an inclined plane is perpendicular to its projection, then it is perpendicular to the inclined one. And vice versa: If a straight line in a plane is perpendicular to an inclined one, then it is also perpendicular to the projection of the inclined one. A dihedral angle is a figure formed by two half-planes with a common straight line limiting them. Half-planes are called faces, and the straight line limiting them is an edge of a dihedral angle. SIGN OF PERPENDICULARITY OF PLANES. If a plane passes through a line perpendicular to another plane, then these planes are perpendicular. A prism is a polyhedron, two of whose faces are congruent (equal) polygons lying in parallel planes, and the remaining faces are parallelograms having common sides with these polygons. Types of prisms: A straight prism is a prism in which all the side edges are perpendicular to the base, otherwise the prism is called an inclined prism. The area of the lateral surface of a straight prism is equal to the product of the perimeter of the base and the length of the lateral edge (or height). In a straight prism, the lateral edges are the heights. The area of the lateral surface of an inclined prism is equal to the product of the perpendicular section perimeter and the length of the lateral edge. The volume of an inclined prism is equal to the product of the perpendicular cross-sectional area and the lateral edge. Regular prism - a prism at the base of which lies a regular polygon, and the side edges are perpendicular to the planes of the base. The bases of a regular prism are regular polygons. The lateral faces of a regular prism are equal rectangles. The lateral edges of a regular prism are equal. A correct prism is straight. A regular prism, the side faces of which are squares (the height of which is equal to the side of the base), is a semi-regular polyhedron. The area of the lateral surface of an arbitrary prism, where P is the perpendicular section perimeter, l is the length of the side edge. A truncated pyramid is a polyhedron whose vertices are the vertices of the base and the vertices of its section by a plane parallel to the base. Prism volume: V = S bases H The volume of a rectangular parallelepiped is equal to the product of the area of the base and the height: V= SH= abc The volume of the pyramid is equal to one third of the product of the base area and the height: where S is the base area, H is the height of the pyramid. The volume V of a truncated pyramid can be found by the formula where H is the height of the truncated pyramid, S1 and S2 are the areas of its bases. Cylinder (ancient Greek κύλινδρος - roller, roller) - geometric body, bounded by a cylindrical surface and two parallel planes intersecting it. A cylindrical surface is a surface obtained by forward movement line (generator) in space, that the selected point of the generator moves along a plane curve (director). The cross section of a cylinder with a plane parallel to its axis is a rectangle. The axial section is the section that passes through the axis of the cylinder. Lateral surface area cylinder is equal to the product of the circumference of the base and the height: S=2π rh Total area surfaces cylinder: Section of a cylinder. A cone is a body obtained by combining all rays emanating from one point (the vertex of the cone) and passing through a flat surface. Cone area: A truncated cone is a body of revolution formed by the rotation of a rectangular trapezoid about the side perpendicular to the bases. Surface area of a truncated cone: S=π(r12+(r1+ r2) l+ r22) A ball is a body bounded by a spherical surface. Sphere (Greek σφαῖρα - ball) is a closed surface, the geometric locus of points in space equidistant from a given point, called the center of the sphere. Sphere area: Spherical surface area spherical sector: , where H is the height of the segment. A cylinder (ancient Greek κύλινδρος - roller, roller) is a geometric body bounded by a cylindrical surface and two parallel planes intersecting it. Cone: Truncated cone: V=1/3π h(r 2 +r 1 ·r 2 +r 2 2) Truncated cone (Fig. 1.20) Ball segment volume: Ball sector volume: Properties: · The parallelepiped is symmetrical about the middle of its diagonal. · Any segment with ends belonging to the surface of the parallelepiped and passing through the middle of its diagonal is divided in half by it; in particular, all diagonals of a parallelepiped intersect at one point and are bisected by it. · Opposite faces of a parallelepiped are parallel and equal. Square of the length of the diagonal of a rectangular parallelepiped equal to the sum squares of its three dimensions. We present a summary table for convenience and clarity when studying the topic. Constanty = C Power function y = x p (x p) " = p x p - 1 Exponential functiony = a x (a x) " = a x ln a In particular, whena = ewe have y = e x (e x) " = e x Logarithmic function (log a x) " = 1 x ln a In particular, whena = ewe have y = logx (ln x) " = 1 x Trigonometric functions (sin x) " = cos x (cos x) " = - sin x (t g x) " = 1 cos 2 x (c t g x) " = - 1 sin 2 x Inverse trigonometric functions (a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2 Hyperbolic functions (s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 s h 2 x Let us analyze how the formulas of the specified table were obtained or, in other words, we will prove the derivation of derivative formulas for each type of function. In order to withdraw this formula, let us take as a basis the definition of the derivative of a function at a point. We use x 0 = x, where x takes the value of any real number, or, in other words, x is any number from the domain of the function f (x) = C. Let's write down the limit of the ratio of the increment of a function to the increment of the argument as ∆ x → 0: lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0 Please note that the expression 0 ∆ x falls under the limit sign. It is not the uncertainty “zero divided by zero,” since the numerator does not contain an infinitesimal value, but precisely zero. In other words, the increment of a constant function is always zero. So, the derivative of the constant function f (x) = C is equal to zero throughout the entire domain of definition. Example 1 The constant functions are given: f 1 (x) = 3, f 2 (x) = a, a ∈ R, f 3 (x) = 4. 13 7 22 , f 4 (x) = 0 , f 5 (x) = - 8 7 Solution
Let's describe given conditions. In the first function we see the derivative of the natural number 3. In the following example, you need to take the derivative of A, Where A- any real number. The third example gives us the derivative of the irrational number 4. 13 7 22, the fourth is the derivative of zero (zero is an integer). Finally, in the fifth case we have the derivative of the rational fraction - 8 7. Answer: derivatives of given functions are zero for any real x(over the entire definition area) f 1 " (x) = (3) " = 0 , f 2 " (x) = (a) " = 0 , a ∈ R , f 3 " (x) = 4 . 13 7 22 " = 0 , f 4 " (x) = 0 " = 0 , f 5 " (x) = - 8 7 " = 0 Let's move on to the power function and the formula for its derivative, which has the form: (x p) " = p x p - 1, where the exponent p is any real number. Evidence 2 Let us give a proof of the formula when the exponent is natural number: p = 1, 2, 3, … We again rely on the definition of a derivative. Let's write down the limit of the ratio of the increment of a power function to the increment of the argument: (x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x To simplify the expression in the numerator, we use Newton’s binomial formula: (x + ∆ x) p - x p = C p 0 + x p + C p 1 · x p - 1 · ∆ x + C p 2 · x p - 2 · (∆ x) 2 + . . . + + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p - x p = = C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p Thus: (x p) " = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + ... + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 + C p 2 x p - 2 ∆ x + . . + C p p - 1 x (∆ x) p - 2 + C p p (∆ x) p - 1) = = C p 1 · x p - 1 + 0 + 0 + . . . + 0 = p ! 1 ! · (p - 1) ! · x p - 1 = p · x p - 1 Thus, we have proven the formula for the derivative of a power function when the exponent is a natural number. Evidence 3 To provide evidence for the case when p- any real number other than zero, we use the logarithmic derivative (here we should understand the difference from the derivative of a logarithmic function). To have a more complete understanding, it is advisable to study the derivative of a logarithmic function and additionally understand the derivative of an implicit function and the derivative of a complex function. Let's consider two cases: when x positive and when x negative. So x > 0. Then: x p > 0 . Let us logarithm the equality y = x p to base e and apply the property of the logarithm: y = x p ln y = ln x p ln y = p · ln x At this stage, we have obtained an implicitly specified function. Let's define its derivative: (ln y) " = (p · ln x) 1 y · y " = p · 1 x ⇒ y " = p · y x = p · x p x = p · x p - 1 Now we consider the case when x – a negative number. If the indicator p is an even number, then the power function is defined for x< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1 Then x p< 0 и возможно составить доказательство, используя логарифмическую производную. If p is an odd number, then the power function is defined for x< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции: y " (x) = (- (- x) p) " = - ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p x p - 1 The last transition is possible due to the fact that if p is an odd number, then p - 1 either an even number or zero (for p = 1), therefore, for negative x the equality (- x) p - 1 = x p - 1 is true. So, we have proven the formula for the derivative of a power function for any real p. Example 2 Functions given: f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 - 1 4 , f 3 (x) = 1 x log 7 12 Determine their derivatives. Solution
We transform some of the given functions into tabular form y = x p , based on the properties of the degree, and then use the formula: f 1 (x) = 1 x 2 3 = x - 2 3 ⇒ f 1 " (x) = - 2 3 x - 2 3 - 1 = - 2 3 x - 5 3 f 2 " (x) = x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3" ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84 Let us derive the derivative formula using the definition as a basis: (a x) " = lim ∆ x → 0 a x + ∆ x - a x ∆ x = lim ∆ x → 0 a x (a ∆ x - 1) ∆ x = a x lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0 We got uncertainty. To expand it, let's write a new variable z = a ∆ x - 1 (z → 0 as ∆ x → 0). In this case, a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . For the last transition, the formula for transition to a new logarithm base was used. Let us substitute into the original limit: (a x) " = a x · lim ∆ x → 0 a ∆ x - 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z Let us remember the second remarkable limit and then we obtain the formula for the derivative exponential function: (a x) " = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a Example 3 The exponential functions are given: f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x It is necessary to find their derivatives. Solution
We use the formula for the derivative of the exponential function and the properties of the logarithm: f 1 " (x) = 2 3 x " = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 " (x) = 5 3 x " = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 " (x) = 1 (e) x " = 1 e x " = 1 e x ln 1 e = 1 e x ln e - 1 = - 1 e x Let us provide a proof of the formula for the derivative of a logarithmic function for any x in the field of definition and any acceptable values base a of the logarithm. Based on the definition of derivative, we get: (log a x) " = lim ∆ x → 0 log a (x + ∆ x) - log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a From the indicated chain of equalities it is clear that the transformations were based on the property of the logarithm. The equality lim ∆ x → 0 1 + ∆ x x x ∆ x = e is true in accordance with the second remarkable limit. Example 4 Logarithmic functions are given: f 1 (x) = log ln 3 x , f 2 (x) = ln x It is necessary to calculate their derivatives. Solution
Let's apply the derived formula: f 1 " (x) = (log ln 3 x) " = 1 x · ln (ln 3) ; f 2 " (x) = (ln x) " = 1 x ln e = 1 x So, the derivative of the natural logarithm is one divided by x. Let's use some trigonometric formulas and the first remarkable limit to derive the formula for the derivative of a trigonometric function. According to the definition of the derivative of the sine function, we get: (sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x The formula for the difference of sines will allow us to perform the following actions: (sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 Finally, we use the first wonderful limit: sin " x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x So, the derivative of the function sin x will cos x. We will also prove the formula for the derivative of the cosine: cos " x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x Those. the derivative of the cos x function will be – sin x. We derive the formulas for the derivatives of tangent and cotangent based on the rules of differentiation: t g " x = sin x cos x " = sin " x · cos x - sin x · cos " x cos 2 x = = cos x · cos x - sin x · (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g " x = cos x sin x " = cos " x · sin x - cos x · sin " x sin 2 x = = - sin x · sin x - cos x · cos x sin 2 x = - sin 2 x + cos 2 x sin 2 x = - 1 sin 2 x Derivative Section inverse functions provides comprehensive information on the proof of the formulas for the derivatives of arcsine, arccosine, arctangent and arccotangent, so we will not duplicate the material here. We can derive the formulas for the derivatives of the hyperbolic sine, cosine, tangent and cotangent using the differentiation rule and the formula for the derivative of the exponential function: s h " x = e x - e - x 2 " = 1 2 e x " - e - x " = = 1 2 e x - - e - x = e x + e - x 2 = c h x c h " x = e x + e - x 2 " = 1 2 e x " + e - x " = = 1 2 e x + - e - x = e x - e - x 2 = s h x t h " x = s h x c h x " = s h " x · c h x - s h x · c h " x c h 2 x = c h 2 x - s h 2 x c h 2 x = 1 c h 2 x c t h " x = c h x s h x " = c h " x · s h x - c h x · s h " x s h 2 x = s h 2 x - c h 2 x s h 2 x = - 1 s h 2 x If you notice an error in the text, please highlight it and press Ctrl+Enter
, where C is an arbitrary constant. The function f(x) is usually called the integrand, the product f(x) dx - the integrand.
If f(x) is continuous and positive on , then the integral is the area of the curved trapezoid bounded by the lines y = 0, x = a, x = b, y = f(x).
or in general
where t is a derived parameter, ax, ay are the x and y coordinates of the directing vector of the straight line, while
; 
Cases of relative position of a straight line and a plane:
If two parallel planes are intersected by a third, then the lines of their intersection are parallel.
Pyramid (ancient Greek πυραμίς, gen. p. πυραμίδος) is a polyhedron, the base of which is a polygon, and the remaining faces are triangles having a common vertex.
A parallelepiped (from the Greek παράλλος - parallel and the Greek επιπεδον - plane) is a prism, the base of which is a parallelogram, or (equivalently) a polyhedron, which has six faces and each of them is a parallelogram.
Derivative of a constant
Evidence 1 Derivative of a power function
Derivative of an exponential function
Proof 4 Derivative of a logarithmic function
Evidence 5 Derivatives of trigonometric functions
Proof 6 Derivatives of inverse trigonometric functions
Derivatives of hyperbolic functions
Evidence 7