Наклонная асимптота y x. Асимптоты

Сколько асимптот может быть у графика функции?

Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса - бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.

Что значит найти асимптоты графика функции?

Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.

Вертикальные асимптоты графика функции

Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.

Примечание: обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой - зависит от контекста.

Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова - любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат.

Из вышесказанного также следует очевидный факт: если функция непрерывна на, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)

Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.

Наклонные асимптоты графика функции

Наклонные (как частный случай - горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при, а график арктангенса при - двумя такими асимптотами, причём различными.

Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью. Например, …правильно догадались: .

Понятие асимптот

Одним из важных этапов построения графиков функций является поиск асимптот. С асимптотами мы встречались неоднократно: при построении графиков функций , y=tgx , y=сtgx . Мы определяли их как линии, к которым «стремится» график функции, но никогда их не пересечет. Пришло время дать точное определение асимптот.

Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная. На чертеже асимптоты принято обозначать пунктирными линиями.

Рассмотрим следующий искусственно составленный график функции (рис. 16.1), на примере которого хорошо видны все виды асимптот:

Дадим определение каждому виду асимптот:

1. Прямая х=а называется вертикальной асимптотой функции , если .

2. Прямая у=с называется горизонтальной асимптотой функции , если .

3. Прямая у=kx+b называется наклонной асимптотой функции , если .

Геометрически определение наклонной асимптоты означает, что при →∞ график функции сколь угодно близко подходит к прямой у=kx+b , т.е. они практически совпадают. Разность практически одинаковых выражений стремится к нулю.

Отметим, что горизонтальные и наклонные асимптоты рассматриваются только при условии →∞. Иногда их различают на горизонтальные и наклонные асимптоты при →+∞ и →-∞.

Алгоритм поиска асимптот

Для поиска асимптот можно использовать следующий алгоритм:

Вертикальных асимптот может быть одна, несколько или не быть совсем.

• Если с – число, то у=с – горизонтальная асимптота;
• Если с – бесконечность, то горизонтальных асимптот нет.

Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем – их нет.

Рассмотрим примеры нахождения асимптот функции:

Пример 16.1. Найдите асимптоты кривой .

Решение х -1≠0; х ≠1.

Проверим, является ли прямая х= 1 вертикальной асимптотой. Для этого вычислим предел функции в точке х= 1: .

х= 1 - вертикальная асимптота.

с = .

с = = . Т.к. с =2 (число), то у=2 – горизонтальная асимптота.

Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.

х= 1 и горизонтальную асимптоту у=2. Для наглядности график данной функции представлен на рис. 16.2.

Пример 16.2 . Найдите асимптоты кривой .

Решение . 1. Найдем область определения функции: х -2≠0; х ≠2.

Проверим, является ли прямая х= 2 вертикальной асимптотой. Для этого вычислим предел функции в точке х= 2: .

Получили, что , следовательно, х= 2 - вертикальная асимптота.

2. Для поиска горизонтальных асимптот находим : с = .

Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с = = . Т.к. с – бесконечность, то горизонтальных асимптот нет.

3. Для поиска наклонных асимптот находим :

Получили неопределенность вида , воспользуемся правилом Лопиталя: = =1.Итак, 1. Найдем b по формуле: .

b= = =

Получили, что b= 2. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+2.

Рис. 16.3

Таким образом, данная функция имеет вертикальную асимптоту х= 2 и наклонную асимптоту у=x+2. Для наглядности график функции представлен на рис. 16.3.

Контрольные вопросы:

Лекция 17. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЯ ГРАФИКА

В данной лекции мы подведем итог всему ранее изученному материалу. Конечная цель нашего долгого пути – уметь исследовать любую аналитически заданную функцию и строить ее график. Важными звеньями нашего исследования будут исследование функции на экстремумы, определение интервалов монотонности, выпуклости и вогнутости графика, поиск точек перегиба, асимптот графика функции.

С учетом всех вышеперечисленных аспектов приведем схему исследования функции и построения графика .

1. Найти область определения функции.

2. Исследовать функцию на четность-нечетность:

· если , то функция четная (график четной функции симметричен относительно оси Оу );

· если , то функция нечетная (график нечетной функции симметричен относительно начала координат);

· в противном случае функция ни четная, ни нечетная.

3. Исследовать функцию на периодичность (среди изучаемых нами функций периодическими могут быть только тригонометрические функции).

4. Найти точки пересечения графика функции с осями координат:

· Ох : у =0 (решаем уравнение лишь в том случае, если можем использовать известные нам методы);

· Оу : х =0.

5. Найти первую производную функции и критические точки первого рода.

6. Найти интервалы монотонности и экстремумы функции.

7. Найти вторую производную функции и критические точки второго рода.

8. Найти интервалы выпуклости-вогнутости графика функции и точки перегиба.

9. Найти асимптоты графика функции.

10. Построить график функции. При построении следует учесть случаи возможного расположения графика вблизи асимптот :

11. При необходимости выбрать контрольные точки для более точного построения.

Рассмотрим схему исследования функции и построения ее графика на конкретных примерах:

Пример 17.1 . Постройте график функции .

Решение . 1. Данная функция определена на всей числовой прямой за исключением х =3, т.к. в этой точке знаменатель обращается в ноль.

2. Для определения четности и нечетности функции найдем :

Видим, что и , следовательно, функция ни четная, ни нечетная.

3. Функция непериодическая.

4. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью Ох примем у =0. Получим уравнение: . Итак, точка (0; 0) – точка пересечения с осями координат.

5. Найдем производную функции по правилу дифференцирования дроби: = = = = .

Для нахождения критических точек найдем точки, в которых производная функции равна 0 или не существует.

Если =0, следовательно, . Произведение тогда равно 0, когда хотя бы один из множителей равен 0: или .

х -3) 2 равен 0, т.е. не существует при х =3.

Итак, функция имеет три критические точки первого рода: ; ; .

6. На числовой оси отметим критические точки первого рода, причем точку отмечаем выколотой точкой, т.к. в ней функция не определена.

Расставляем знаки производной = на каждом промежутке:

т.min

т.max

На промежутках, где , исходная функция возрастает (при (-∞;0] ), где - убывает (при ).

Точка х =0 является точкой максимума функции. Для нахождения максимума функции найдем значение функции в точке 0: .

Точка х =6 является точкой минимума функции. Для нахождения минимума функции найдем значение функции в точке 6: .

Результаты исследований можно занести в таблицу. Число строк в таблице фиксировано и равно четырем, а число столбцов зависит от исследуемой функции. В ячейки первой строки последовательно заносят интервалы, на которые критические точки разбивают область определения функции, включая сами критические точки. Во избежание ошибок при построении точки, не принадлежащие области определения, можно в таблицу не включать.

Во второй строке таблицы расставляются знаки производной на каждом из рассматриваемых промежутков и значение производной в критических точках. В соответствии со знаками производной функции в третьей строке отмечаются промежутки возрастания, убывания, экстремумы функции.

Последняя строка служит для обозначения максимума и минимума функции.

х	(-∞;0)		(0;3)		(3;6)		(6;+ ∞)
	+		-		-		+
f(x)
Выводы		max				min

7. Найдем вторую производную функции как производную от первой производной: = =

Вынесем в числителе х -3 за скобки и выполним сокращение:

Приведем в числителе подобные слагаемые: .

Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.

0, если =0. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.

Не существует, если знаменатель (х -3) 3 равен 0, т.е. не существует при х =3. :Ох , Оу , начало отсчета, единицы измерения по каждой оси.

Прежде чем строить график функции, нужно:

· провести асимптоты пунктирными линиями;

· отметить точки пересечения с осями координат;

Рис. 17.1

отметить максимум и минимум функции, причем рекомендуется прямо на чертеже обозначить максимум и минимум функции дугами: k или ;

· пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, построить график функции. Ветви графика должны «стремиться» к асимптотам, но их не пересекать.

· проверить, соответствует ли график функции проведенному исследованию: если функция четная или нечетная, то соблюдена ли симметрия; соответствуют ли теоретически найденным промежутки возрастания и убывания, выпуклости и вогнутости, точки перегиба.

11. Для более точного построения можно выбрать несколько контрольных точек. Например, найдем значения функции в точках -2 и 7:

Корректируем график с учетом контрольных точек.

Контрольные вопросы:

Каков алгоритм построения графика функции?

Может ли функция иметь экстремум в точках, не принадлежащих области определении?

ГЛАВА 3. 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.

Регистрация участников открыта. Получите свой билет на Марс по этой ссылке .

Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.

Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.

Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.

Очередной канун Нового Года... морозная погода и снежинки на оконном стекле... Все это побудило меня вновь написать о... фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.

Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.

Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: "Фракталы - это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией".

Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.

Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное возможное расстояние, но так и не касается его.

Определение 1. Асимптотами называются такие прямые , к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.

Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты

Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy .

Определение . Прямая x = a является вертикальной асимптотой графика функции , если точка x = a является точкой разрыва второго рода для этой функции.

Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f (x ) , если выполняется хотя бы одно из условий:

При этом функция f (x ) может быть вообще не определена соответственно при x ≥ a и x ≤ a .

Замечание:

Пример 1. График функции y =lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:

(рис. сверху).

самостоятельно, а затем посмотреть решения

Пример 2. Найти асимптоты графика функции .

Пример 3. Найти асимптоты графика функции

Горизонтальные асимптоты

Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox .

Если (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b ), то y = b – горизонтальная асимптота кривой y = f (x ) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).

Пример 5. График функции

при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении "икса" к минус бесконечности равен нулю:

Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении "икса" к плюс бесконечности равен бесконечности:

Наклонные асимптоты

Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число - точка на оси абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше - угловой коэффициент k , который показывает угол наклона прямой, и свободный член b , который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё - уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом . Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.

Теорема. Для того, чтобы кривая y = f (x ) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:

(1)

(2)

Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.

В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.

При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.

При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.

Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).

Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .

Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

Пример 6. Найти асимптоты графика функции

Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.

Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:

Следовательно, x = 0 – вертикальная асимптота графика данной функции.

Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:

Выясним наличие наклонной асимптоты:

Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).

Пример 7. Найти асимптоты графика функции

Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:

Заключение: x = −1 - точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.

Ищем наклонные асимптоты. Так как данная функция - дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой - наклонной асимптоты:

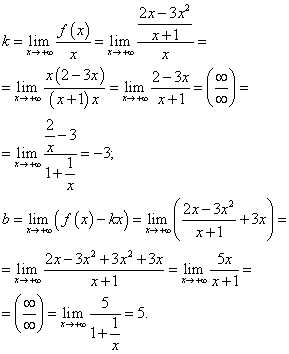
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:

y = −3x + 5 .

На рисунке график функции обозначен бордовым цветом, а асимптоты - чёрным.

Пример 8. Найти асимптоты графика функции

Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:

.

Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .

Пример 9. Найти асимптоты графика функции

Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .

Рассмотрим правосторонний предел при (левосторонний предел не существует):

.

Точка x = 2 - точка разрыва второго рода, поэтому прямая x = 2 - вертикальная асимптота графика данной функции.

Ищем наклонные асимптоты:

Итак, y = x + 1 - наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :

Итак, y = −x − 1 - наклонная асимптота при .

Пример 10. Найти асимптоты графика функции

Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при .

Определение . Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точкиграфика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат .

По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные, наклонные.

Очевидно, горизонтальные являются частными случаями наклонных (при ).

Нахождение асимптот графика функции основано на следующих утверждениях.

Теорема 1 . Пусть функция определена хотя бы в некоторой полуокрестности точкии хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равенили. Тогда прямаяявляется вертикальной асимптотой графика функции .

Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).

Теорема 2 . Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции. Тогда прямаяесть горизонтальная асимптота графика функции.

Может случиться, что , а, причеми- конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов или, то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.

Теорема 3 . Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределыи. Тогда прямаяявляется наклонной асимптотой графика функции .

Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.

Наклонная асимптота так же, как и горизонтальная, может быть односторонней.

Пример . Найдите все асимптоты графика функции .

Решение .

Функция определена при . Найдем ее односторонние пределы в точках.

Так как и(два других односторонних предела можно уже не находить), то прямыеиявляются вертикальными асимптотами графика функции.

Вычислим

(применим правило Лопиталя) =.

Значит, прямая - горизонтальная асимптота.

Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).

Ответ : график имеет две вертикальные асимптоты и одну горизонтальную.

Общие исследование функции y = f (x ).

Область определения функции. Найти ее область определения D (f ) . Если это не слишком сложно, то полезно найти также область значений E (f ) . (Однако, во многих случаях, вопрос нахождения E (f ) откладывается до нахождения экстремумов функции.)

Особые свойства функции. Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox . Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.

Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определенияD (f ), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.

Наклонные и горизонтальные асимптоты. Если область определения D (f ) вклоючает в себя лучи вида (a;+) или (−;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x+или x−соответственно, т.е. найти limxf(x).Наклонные асимптоты : y = kx + b, где k=limx+xf(x) и b=limx+(f(x)−x).Горизонтальны асимптоты : y = b, где limxf(x)=b.

Нахождение точек пересечения графика с осями . Нахождение точки пересечения графика с осью Oy . Для этого нужно вычислить значение f (0). Найти также точки пересечения графика с осью Ox , для чего найти корни уравнения f (x ) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.

Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.

Нахождение интервалов выпуклости и вогнутости . Это делается с помощью исследования знака второй производной f(x). Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции. Найдя f(x) , мы решаем неравенство f(x)0. На каждом из интервалов решения функция будет выпуклой вниз. Решая обратное неравенство f(x)0, мы находим интервалы, на которых функция выпукла вверх (то есть вогнута). Определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).