Расчёт опорных реакций. Опоры и опорные реакции

Пример1.

Примеры выполнения задания (при действии на балку равномерно распределенной нагрузки и сосредоточенных сил и моментов).

Разберем на конкретных примерах построение эпюр для балок, находящихся под действием равномерно распределенной нагрузки и сосредоточенных сил и моментов, расположенных в одной плоскости.

Построить эпюры поперечных сил и изгибающих моментов для боевой оси круглого поперечного сечения ГМ-30, изображенного на рис.1

Дано:

[σ]=21000 kH/м 2

Определить из расчета на прочность размеры поперечного сечения оси.

Решение:

Отбрасывают опоры А и В, а их действие на балку заменяют реакциями опор R A и R B .

Направление опорных реакций выбирают положительным, т.е. направленным вверх. Если в результате расчета значение какой-либо реакции получается отрицательным, то это означает, что в действительности ее направление противоположно предварительно принятому, для чего необходимо поменять направление этой реакции и считать ее далее положительной.

Так как балка под действием приложенных к ней сил и моментов находится в равновесии, то для нее справедливы следующие три уравнения статики:

1 уравнение: :

где – равнодействующая распределенной нагрузки интенсивностью на длине балки « », - плечо этой равнодействующей относительно точки А.

Из уравнения 1 имеем:

рис.1 Расчетная схема балки и эпюры и

2 уравнение : (2)

3 уравнение – сумма моментов всех сил относительно точки В – используют для проверки правильности найденных значений реакций.

Подставив значения получим , т.е. составленное уравнение удовлетворяется, это указывает на правильность определения опорных реакций:

Примечание:

3. Момент считается положительным, если направлен против часовой стрелки, и отрицательным, если направлен по часовой стрелке.

4. Сила положительна, если направлена по оси «Y» вверх, и отрицательна, если направлена вниз.

3.3.1.2. Построение эпюр и .

Балку разбивают на участки I и II и для каждого участка составляют аналитические зависимости изменения внутренних силовых факторов, с помощью которых производят построение эпюр и .

На участке балки на расстоянии от левого конца проводят сечение и рассматривают равновесие левой части балки. Составляют уравнение для поперечной силы и изгибающего момента :

Выражение для силы представляет собой уравнение прямой, параллельной оси абсцисс. Зависимость от линейная, поэтому для построения эпюры на участке I достаточно определить величины при двух значениях аргумента :

1) при (в начале участка I);

2) при м (в конце участка I);

По полученным значениям и на рис.1 строят эпюры и для первого участка балки.

Примечание:

1. Знак «плюс» перед значением реакций свидетельствует о том, что принятое направление реакций соответствует их действительному направлению.

2. В случае отрицательного значения реакции необходимо изменять направление этой реакции на расчетной схеме и далее принимать ее значение положительным.

На участке II балки на расстоянии от правого конца балки проводят поперечное сечение и рассматривают равновесие отсечённой правой части балки.

Уравнение для силы на II участке представляет собой уравнение прямой линии, наклонённой к оси абсцисс. Для её построения достаточно знать координаты двух точек (обычно выбирают координаты границ участка).

Проводим через две полученные точки прямую поперечной силы (рис.1), так как прямая эпюры поперечной силы пересекает ось , то в точке пересечения на эпюре изгибающих моментов должен быть экстремум (). Находят координату точки пересечения . Для этого приравнивают выражение поперечной силы (4 ) к нулю, т.е.: .

3.3.1.3. Определение диаметра поперечного сечения .

Для определения диаметра балки используют условие прочности при изгибе , где – осевой момент сопротивления сечения изгибу.

Таким образом определены размеры поперечного сечения оси, исходя из построенных эпюр и .

1. Определим опорные реакции балки. Составим урав­нения:

Из первого уравнения найдем V B:

или –15·2 + 20·6·2 - V B ·7 -25 = 0,

откуда кН.

Из второго уравнения найдем V A:

или –15·9 – 20·6·5 + V А ·7 – 25 = 0,

откуда кН.

Выполним проверку:

или 108,6 + 26,4 – 15 – 20 · 6 = 0,

откуда 135 – 135 = 0.

2. Обозначим характерные сечения балки С, D, А, Е, В, К.

3. Определим значения поперечных сил в характерных сечениях:

Q C = –F = –15 кН;

Q D = –F = –15 кН;

кН;

4. Строим эпюру Q x . Соединим полученные значения прямыми линиями (рис. 11, б) и получим эпюру Q x . Эпюра Q x на участке АЕ пересекает нулевую линию. Определим положение точки, в которой эпюра Q x пересекает нулевую линию. Рассмотрим подобие треугольников HRL и HNS (см. рис. 11, б), откуда HR/HN = HL/HS, или х 0 /5 = = 73,6/100, откуда

м.

Это сечение считается также характерным для эпюры Q x и М х.

5. Определим изгибающие моменты в ха­рактерных точках:

= –15 · 5,68 – 20 · 4,68 · 2,34 + 108,6 · 3,68 = 95,4 кН м;

М В = М = 25 кН м (рассмотрена правая часть балки ВК );

М К = М = 25 кН м.

6. Строим эпюру М х на участках между характерными точка­ми:

а) на участке CD нагрузки нет, поэтому эпюра М х - прямая линия, соединяющая значения М С =0и М D = –15 кН м;

б) на участке DA М х - парабола.

Так как эпюра Q x на этом участке не пе­ресекает нулевую линию, то парабола не имеет экстремального значения, поэтому величины изгибающих моментов в сечениях D и А соединим кривой, значения которой находятся в интервале –15 кН м... – 40 кН м;

в) на участке АЕ действует распределенная нагрузка, поэтому эпюра М х - парабола. Так как эпюра Q x на этом участке пересе­кает нулевую линию, то парабола имеет экстремальное значение (вершину), поэтому эпюру М х строим по трем значениям:

М А = – 40 кН м; М х 0 = 95,4 кН м и М Е = 78 кН м;

д) на участке ВК нет нагрузки, поэтому эпюра М х - прямая ли­ния, соединяющая значения М В = 25 кН м и М К =25 кН м.

Эпюра М х построена (рис. 11, в).

В качестве проверки возьмем сумму моментов всех сил отно­сительно точки, расположенной на расстоянии х 0 от левой опо­ры, но рассмотрим правую часть балки:

M х 0 = q (c – х 0)(с – х 0)/2 + V B (с – х 0 + d )+ М =

=–20 · 1,32 · 0,66 + 26,4 · 3,32 + 25 = 95,3 кН.

Разница в значениях М х при рассмотрении левых и правых сил возможна из-за округления величин опорных реакций и рас­стояния х 0 .

7. Подберем сечение стальной двутавровой балки по наибольше­му изгибающему моменту

По табл. 1 прил. I принимаем двутавровую балку №30 с W x =472 см 3 , что больше, чем W x т p =415 см 3 .

8. Проверим прочность принятого сечения:

Прочность сечения по нормальным напряжениям обеспечена.

Ответ: двутавровая балка № 30.

Задание для практического решения №4. Для балки на двух опорах, показанной на рис. 12, определить опорные реакции, проверить правильность определения реакций. Определить значения внутренних поперечных сил в характерных сечениях балки. Построить эпюру поперечных сил.

Определить значения внутренних изгибающих моментов в характерных сечениях балки. Построить эпюру изгибающих моментов. Подобрать рациональное сечение двутавровой балки, если [σ] = 160 МПа. Проверить прочность выбранного сечения по нормальным.

Рис. 12. Продолжение

Рис. 12. Продолжение

Рис. 12. Продолжение

Рис. 12. Окончание

Контрольные вопросы

1) При каких внутренних силовых факторах в поперечном сечении бруса возникает деформация, названная чистым изгибом? Поперечным изгибом?

2) Как определить в любом поперечном сечении бруса величину поперечной силы и величину изгибающего момента?

3) Сформулируйте правило знаков при определении поперечной силы и изгибающих моментов?

4) Что такое эпюры поперечных сил и изгибающих моментов? Как и для чего они строятся?

5) На каких допущениях основаны выводы расчетных формул при изгибе?

6) По какой формуле определяют нормальные напряжения в поперечном сечении балки при изгибе и как они меняются по высоте балки?

7) Что такое осевой момент сопротивления сечения? Какова его физическая сущность и единицы измерения?

8) Какие формы поперечного сечения являются рациональными для балок из пластичных материалов и для балок из хрупких материалов?

9) Какие виды расчета можно производить из условия прочности при изгибе?

10) Почему при изгибе балки в её продольном сечении возникают касательные напряжения?

11) В каких случаях необходимо производить проверку балки по касательным напряжениям?

Лекция №3

Тема: « Внутренние усилия в поперечных сечениях стержня»

Вопросы:

1. Опоры и опорные реакции, и их определение

3. Взаимосвязь между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки

1. Опоры и опорные реакции, и их определение

При расчете конструкций в основном встречаются элементы, испытывающие изгиб. Стержни, работающие преимущественно на изгиб, называют балками. Для того чтобы балка могла испытывать нагрузку и передавать ее на основание, она должна быть соединена с ним опорными связями. На практике применяют несколько типов опорных связей, или, как говорят, несколько типов опор.

Различают три основных типа опор:

а) шарнирно-подвижная опора:

б) шарнирно-неподвижная опора:

в) жесткая заделка.

Рис. 1

На рис. 1 показана шарнирно-подвижная опора, такая опора позволяет балке свободно поворачиваться и перемещаться в горизонтальном направлении. Поэтому реакция в опоре будет одна  вертикальная сила. Условное обозначение такой опоры показано справа.

Рис. 2

На рис. 2 показана шарнирно-неподвижная опора. Такая опора позволяет балке свободно поворачиваться, но перемещаться она не может. Поэтому могут возникать две реакции - вертикальная и горизонтальная силы. Их можно сложить и получить одну результатирующую силу, но нужно знать угол, под которым oна будет направлена. Более удобно будет пользоваться вертикальной и горизонтальной составляющими реакции.

На рис. 3 показана жесткая заделка. Она не позволяет балке ни поворачиваться, ни перемещаться. Поэтому могут возникать три опорные реакции: момент, вертикальная и горизонтальная силы. Если балка не имеет на конце опоры, то эта часть ее называется консолью.

Рис. 3

Определим реакции опор для балки (см. рис. 4).

Рис.4

В опоре А горизонтальная реакция равна нулю, так как распределенная нагрузка q и сосредоточенная сила F имеют вертикальное направление. Реакции опор
направим вверх. Составим два уравнения статического равновесия сил. Сумма моментов относительно каждой из опор равна нулю. Уравнения моментов нужно составлять относительно опор, так как в этом случае получаются уравнения с одним неизвестным. Если составить уравнения относительно точек В и С, то получим уравнения с двумя неизвестными, а их решать сложнее. Моменты против часовой стрелки будем считать положительными, по часовой  отрицательными.

где
 момент от равномерно распределенной нагрузки.

Произведение q на расстояние, на котором она приложена, из условия равновесия системы равно сосредоточенной силе, приложенной посредине отрезка. Поэтому момент
равен:

– момент силы F

Внешний момент m на плечо не умножается, так какэто пара сил, т.е. две равные по величине, противоположно направленные силы, имеющие постоянное плечо.

.

Проверка: Сумма всех сил на вертикальную ось Y должна быть равна нулю:

.

Момент m в условие статического равновесия
не записывают, так как момент  это две равные по величине, противоположно направленные силы и в проекции на любую ось они дадут ноль.

30-20-2-40+50=0:

80-80=0.

Реакции определены правильно.

2. Поперечная сила и изгибающий момент

Пусть на балку действуют силы
, реакции опор
. Определим внутренние усилия в сечении, расположенном на расстоянии от нулевого конца (см. рис.5).

Рис. 5

Поскольку все внешние силы действуют вертикально, то горизонтальной составляющей у реакции опоры А не будет. Балка не будет сжиматься или растягиваться, т.е. продольная сила в поперечных сечениях равна нулю. Можно было взять пример, когда силы
были бы не вертикальными по направлению. Тогда бы в опоре А была бы и вторая реакция  горизонтальная сила, а в сечениях балки  продольная сила N . В этом случае балка испытывала бы изгиб с растяжением (сжатием), т.e. был бы случай сложного сопротивления. Его мы будем изучать позднее. Вначале рассматривают более простые задачи и идут к более сложным, а не наоборот.

Поскольку внешние силы
лежат в одной плоскости, проходящей через ось бруса, то возможно возникновение тpex внутренних усилий: изгибающею момента М , поперечной силы Q и продольной силы N , которая, как мы отмечали, равна нулю. Значения М и Q определим из уравнения статического равновесия левой части балки:

Вывод: поперечная сила в сечении численно равна алгебраической сумме всех внешних сил, а изгибающий момент  сумме всех моментов, вычисленных относительно сечения и приложенных к рассматриваемой части балки.

Для поперечных сил и изгибающих моментов приняты обязательные правила знаков (см. рис. 6).

Если сила пытается повернуть рассматриваемую часть балки по часовой стрелке, то она вызывает положительную поперечную силу, и, наоборот, если действует против часовой стрелки  то поперечная сила отрицательная. На рис. 5 сила
вызывает положительное Q , а  отрицательное. Следует отметить, что направление силы положительное для левой части будет отрицательным для правой части. Это вызвано тем, что внутренние силы, действующие на правую и левую часть балки обязательно должны быть равны и противоположно направлены.

Если внешняя сила или внешний момент изгибают балку выпуклостью вниз, то возникающий изгибающий момент положительный и, наоборот, выпуклостью вверх  отрицательный.

Рис. 6

3. Взаимосвязь между изгибающим моментом,

поперечной силой и интенсивностью распределенной нагрузки

Пусть на консольную балку (см. рис. 7) действует распределенная нагрузка, изменяющаяся по длине балки. На расстоянии z от левого конца возьмем бесконечно малый отрезок dz .

Рис. 7

Тогда распределенную нагрузку на нем можно рассматривать как постоянную. В левой части рассматриваемого отрезка будут внутренние усилия Q и М , в правой  с учетом приращения внутренних усилий Q + dQ и M + dM .

Составим уравнения статического равновесия для отрезка балки:

(1)

Третьим членом можно пренебречь, как бесконечно малой величиной более высокого порядка, т.е.:

После преобразований получим:

(2)

т.е. первая производная от изгибающего момента по абсциссе (длине балки) есть поперечная сила.

Если в формулу (1) подставить значение Q из формулы (2), то получим:

, (3)

т.е. вторая производная от изгибающего момента есть интенсивность распределенной нагрузки.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО СТАТИКЕ

Пример 1. Определить реакции опор горизонтальной балки от заданной нагрузки.

Дано:

Схема балки (рис. 1).

P = 20 кН, G = 10 кН, М = 4 кНм, q = 2 кН/м, a =2 м, b =3 м, .

___________________________________

А и В .

Рис. 1

Решение:

Рассмотрим равновесие балки АВ (рис. 2).

К балке приложена уравновешенная система сил, состоящая из активных сил и сил реакции.

Активные (заданные) силы:

Пара сил с моментом М , где

Сосредоточенная сила, заменяющая действие распределенной вдоль отрезка АС нагрузки интенсивностью q .

Величина

Линия действия силы проходит через середину отрезка АС .

Силы реакции (неизвестные силы):

Заменяет действие отброшенного подвижного шарнира (опора А ).

Реакция перпендикулярна поверхности, на которую опираются катки подвижного шарнира.

Заменяют действие отброшенного неподвижного шарнира (опора В ).

Составляющие реакции , направление которой заранее неизвестно.

Расчетная схема

Рис. 2

Для полученной плоской произвольной системы сил можно составить три уравнения равновесия:

Задача является статически определимой, так как число неизвестных сил (,,) - три- равно числу уравнений равновесия.

Поместим систему координат XY в точку А , ось AX направим вдоль балки. За центр моментов всех сил выберем точку В .

Составим уравнения равновесия:

Решая систему уравнений, найдем ,,.

Определив,, найдем величину силы реакции неподвижного шарнира

В целях проверки составим уравнение

Если в результате подстановки в правую часть этого равенства данных задачи и найденных сил реакций получим нуль, то задача решена - верно.

Реакции найдены верно. Неточность объясняется округлением при вычислении .

Ответ:

Пример 2. Для заданной плоской рамы определить реакции опор.

Дано:

Схема рамы рис.3

P = 20 кН, G = 10 кН, М = 4 кНм, q = 2 кН/м, a =2 м, b =3 м, .

______________________________

Определить реакции опор рамы.

Рис. 3

Решение:

Рассмотрим равновесие жесткой рамы АВЕС (рис. 4).

Расчетная схема

Рис. 4

Система сил приложенных к раме состоит из активных сил и сил реакций.

Активные силы:

Пара сил с моментом , , .

, заменяют действие распределенной нагрузки на отрезках ВД и ДЕ .

Линия действия силы проходит на расстоянии от точки В .

Линия действия силы проходит через середину отрезка ДЕ.

Силы реакции:

Заменяют действие жесткого защемления, которое ограничивает любое перемещение рамы в плоскости чертежа.

К раме приложена плоская произвольная система сил. Для нее можем составить три уравнения равновесия:

, ,

Задача является статистически определимой, так как число неизвестных тоже три - , , .

Составим уравнения равновесия, выбрав за центр моментов точку А, так как ее пересекают наибольшее число неизвестных сил.

Решая систему уравнений, найдем , , .

Для проверки полученных результатов составим уравнение моментов вокруг точки С.

Подставляя все значения, получим

Реакции найдены верно.

Ответ:

Пример 3 . Для заданной плоской рамы определить реакции опор.

Дано: вариант расчетной схемы (рис. 5);

Р 1 = 8 кН; Р 2 = 10 кН; q = 12 кН/м; М = 16 кНм; l = 0,1 м.

Определить реакции в опорах А и В .

Рис.5

Решение . Заменяем действие связей (опор) реакциями. Число, вид (сила или пара сил с моментом), а также направление реакций зависят от вида опор. В плоской статике для каждой опоры в отдельности можно проверить, какие направления движения запрещает телу данная опора. Проверяют два взаимно перпендикулярных смещения тела относительно опорной точки (А или В ) и поворот тела в плоскости действия внешних сил относительно этих точек. Если запрещено смещение, то будет реакция в виде силы по этому направлению, а если запрещен поворот, то будет реакция в виде пары сил с моментом (М А или М В).

Первоначально реакции можно выбирать в любую сторону. После определения значения реакции знак «плюс» у него будет говорить о том, что направление в эту сторону верное, а знак «минус» – о том, что правильное направление реакции противоположно выбранному (например, не вниз, а вверх для силы или по часовой стрелке, а не против неё для момента пары сил).

Исходя из вышесказанного, показаны реакции на рис. 5. В опоре А их две, т. к. опора запрещает перемещение по горизонтали и вертикали, а поворот вокруг точки А - разрешает. Момент М А не возникает, т. к. эта шарнирная опора не запрещает поворот телу вокруг точки А . В точке В одна реакция, т. к. запрещено перемещение только в одном направлении (вдоль невесомого рычага ВВ ¢ ).

заменяется эквивалентной сосредоточенной силой . Линия действия её проходит через центр тяжести эпюры (для прямоугольной эпюры центр тяжести на пересечении диагоналей, поэтому сила Q проходит через середину отрезка, на который действует q ). Величина силы Q равна площади эпюры, то есть

Затем необходимо выбрать оси координат x и y и разложить все силы и реакции не параллельные осям на составляющие параллельные им, используя правило параллелограмма. На рис.5 разложены силы , ,. При этом точка приложения результирующей и её составляющих должна быть одна и та же. Сами составляющие можно не обозначать, т. к. их модули легко выражаются через модуль результирующей и угол с одной из осей, который должен быть задан либо определен по другим заданным углам и показан на схеме. Например для силы Р 2 модуль горизонтальной составляющей равен , а вертикальной- .

Теперь можно составить три уравнения равновесия, а так как неизвестных реакций тоже три (,,), их значения легко находятся из этих уравнений. Знак у значения реакции, о чем говорилось выше, определяет правильность выбранных направлений реакций. Для схемы на рис. 5 уравнения проекций всех сил на оси х и y и уравнения моментов всех сил относительно точки А запишутся так:

Из первого уравнения находим значение R B , затем подставляем его со своим знаком в уравнения проекций и находим значения реакций Х А и У А.

В заключение отметим, что удобно уравнение моментов составлять относительно той точки, чтобы в нем оказалась одна неизвестная, т. е. чтобы эту точку пересекали две другие неизвестные реакции. Оси же удобно выбирать так, чтобы большее число сил оказались параллельны осям, что упрощает составление уравнений проекций.

Пример 4. Для заданной конструкции, состоящей из двух ломаных стержней, определить реакции опор и давление в промежуточном шарнире С .

Дано:

Схема конструкции (рис. 6).

P = 20 кН, G = 10 кН, М = 4 кНм, q = 2 кН/м, a =2 м, b =3 м, .

______________________________________

Определить реакции опор в точках А и В и давление в промежуточном шарнире С .

Рис. 6

Решение:

Рассмотрим равновесие всей конструкции (рис. 7).

К ней приложены:

активные силы ,, пара сил с моментом М , где

силы реакции:

, , , ,

Заменяют действие жесткого защемления;

Заменяет действие шарнирно-подвижной опоры А .

Расчетная схема

Рис. 7

Для полученной плоской произвольной системы сил можем составить три уравнения равновесия, а число неизвестных- четыре, , , .

Чтобы задача стала статически определимой, конструкцию расчленяем по внутренней связи - шарниру С и получаем еще две расчетные схемы (рис. 8, рис. 9).

Рис. 8Рис. 9

Заменяют действие тела АС на тело СВ , которое передается через шарнир С . Тело СВ передает свое действие на тело АС через тот же шарнир С , поэтому ; , .

Для трех расчетных схем в сумме можем составить девять уравнений равновесия, а число неизвестных – шесть , , , , , , то есть задача стала статически определима. Для решения задачи используем рис. 8, 9, а рис. 7 оставим для проверки.

Тело ВС (рис. 8)

Тело СА (рис. 9)

4)

5)

6)

Решаем систему шести уравнений с шестью неизвестными.

Проверка:

Реакции внешних опор в точках А и В найдены верно. Давление в шарнире С вычисляем по формуле

Ответ: , , , ,

Минусы означают, что направления инадо изменить на противоположные.

Пример 5. Конструкция состоит из двух частей. Установить, при каком способе соединения частей конструкции модуль реакции наименьший, и для этого варианта соединения определить реакции опор, а также соединения С .

Дано: = 9 кН; = 12 кН; = 26 кНм; = 4 кН/м.

Схема конструкции представлена на рис.10.

Рис.10

Решение:

1) Определение реакции опоры А при шарнирном соединении в точке С.

Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис.11). Составим уравнение моментов сил относительно точки B .

Рис.11

где кН.

После подстановки данных и вычислений уравнение (26) получает вид:

(2)

Второе уравнение с неизвестными и получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира С (рис. 12):

Рис. 12

Отсюда находим, что

кН.

Подставив найденное значение в уравнение (2) найдем значение :

Модуль реакции опоры А при шарнирном соединении в точке С равен:

2) Расчетная схема при соединении частей конструкции в точке С скользящей заделкой, показанной на рис. 13.

Рис. 13

Системы сил, показанные на рис. 12 и 13, ничем друг от друга не отличаются. Поэтому уравнение (2) остается в силе. Для получения второго уравнения рассмотрим систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее скользящей заделки С (рис. 14).

Рис. 14

Составим уравнение равновесия:

и из уравнения (2) находим:

Следовательно, модуль реакции при скользящей заделке в шарнире С равен:

Итак, при соединении в точке С скользящей заделкой модуль реакции опоры А меньше, чем при шарнирном соединении ().

Найдем составляющие реакции опоры В и скользящей заделки.

Для левой от С части

,

Составляющие реакции опоры В и момент в скользящей заделке найдем из уравнений равновесия, составленных для правой от С части конструкции.

кН

Ответ: Результаты расчета приведены в таблице.

							Момент, кНм
	X A	Y A	R A	X C	X B	Y B	M C
Для схемы на рис.11		18,4	19,9
Для схемы на рис.13	14,36	11,09	17,35	28,8	28,8	12,0	17,2

Пример 6.

Дано: вариант расчетной схемы (рис.15).

Р 1 = 14 кН; Р 2 = 8 кН; q = 10 кн/м;М = 6 кНм; АВ = 0,5 м; ВС = 0,4 м; CD = 0,8 м; DE = 0,3 м; EF = 0,6 м.

Определить реакции в опорах А и F .

Решение . Используя рекомендации примера 3, расставляем реакции в опорах. Их получается четыре (, , , ). Так как в плоской статике для одного тела можно составить только три уравнения равновесия, то для определения реакций необходимо разбить конструкцию на отдельные твердые тела так, чтобы число уравнений и неизвестных совпало. В данном случае можно разбить на два тела АВС D и DEF . При этом в месте разбиения, т. е. в точке D для каждого из двух тел появляются дополнительные реакции, определяемые по виду, числу и направлению так же, как и для точек А и F . При этом по третьему закону Ньютона они равны по значению и противоположно направлены для каждого из тел. Поэтому их можно обозначить одинаковыми буквами (см. рис. 16).

Рис. 15

Далее, как и в примере 3, заменяем распределенную нагрузку q сосредоточенной силой и находим её модуль . Затем выбираем оси координат и раскладываем все силы на рис. 15 и 16 на составляющие параллельные осям. После этого составляем уравнения равновесия для каждого из тел. Всего их получается шесть и неизвестных реакций тоже шесть (, , , , , ), поэтому система уравнений имеет решение, и можно найти модули, а с учетом знака модуля и правильное направление этих реакций (см. пример 3).

Рис. 16. Разбиение конструкции на два тела в точке D , т. е. в месте их соединения скользящей заделкой (трение в ней не учитывается)

Целесообразно так выбирать последовательность составления уравнений, чтобы из каждого последующего можно было определить какую-то одну из искомых реакций. В нашем случае удобно начать с тела DEF , т. к. для него имеем меньше неизвестных. Первым составим уравнение проекций на ось х, из которого найдем R F . Далее составим уравнения проекций на оси у и найдем Y D , а затем уравнение моментов относительно точки F и определим M D . После этого переходим к телу ABCD . Для него первым можно составить уравнения моментов относительно точки А и найти М А, а затем последовательно из уравнений проекций на оси найти X A , Y A . Для второго тела необходимо учитывать свои реакции Y D , M D , взяв их из рис.16, но значения этих реакций уже будут известны из уравнений для первого тела.

При этом значения всех ранее определенных реакций подставляются в последующие уравнения со своим знаком. Таким образом, уравнения запишутся так:

для тела DEF

для тела ABCD

В некоторых вариантах задан коэффициент трения в какой-то точке, например . Это означает, что в этой точке необходимо учесть силу трения , где N A реакция плоскости в этой точке. При разбиении конструкции в точке, где учитывается сила трения, на каждое из двух тел действует своя сила трения и реакция плоскости (поверхности). Они попарно противоположно направлены и равны по значению (как и реакции на рис.16).

Реакция N всегда перпендикулярна плоскости возможного скольжения тел либо касательной к поверхностям в точке скольжения, если там нет плоскости. Сила трения же направлена вдоль этой касательной либо по плоскости против скорости возможного скольжения. Приведенная выше формула для силы трения справедлива для случая предельного равновесия, когда скольжение вот-вот начнется (при непредельном равновесии сила трения меньше этого значения, а определяется её величина из уравнений равновесия). Таким образом, в вариантах задания на предельное равновесие с учетом силы трения к уравнениям равновесия для одного из тел необходимо добавить еще одно уравнение . Там, где учитывается сопротивление качению и задан коэффициент сопротивления качения , добавляются уравнения равновесия колеса (рис.17).

При предельном равновесии

Рис.17

Из последних уравнений, зная G , , R , можно найти N , F тр, T для начала качения без проскальзывания.

В заключение отметим, что разбиение конструкции на отдельные тела проводят в том месте (точке), где имеет место наименьшее число реакций. Часто это невесомый трос или невесомый ненагруженный рычаг с шарнирами на концах, которые соединяют два тела (рис 18).

Рис. 18

Пример 7 . Жесткая рама ABCD (рис. 19) имеет в точке А неподвижную шарнирную опору, а в точке б - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

Дано: F =25 кН, =60º , Р =18 кН, =75º , М= 50 кНм, = 30°, а= 0,5 м.

Определить: реакции в точках A и В , вызы­ваемое действующими нагрузками.

Рис. 19

Указания. Задача – на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если составлять уравнение относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы F часто удобно разложить ее на составляющие F ’ и F ”, для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда

Решение. 1. Рассмотрим равновесие пластины. Проведем коорди­натные оси ху и изобразим действующие на пластину силы: силу , пару сил с моментом М, натяжение троса (по модулю T = Р) и реакции связей (реакцию неподвижной шарнирной опоры A изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).

2. Для полученной плоской системы сил составим три уравненияравновесия. При вычислении момента силы относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силуна состав­ляющие F΄ , F ˝ (, ) и учтем, что по теореме Вариньона: Получим:

Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

Ответ: X = -8,5кН; Y = -23,3кН; R = 7,3кН. Знаки указывают, что силы X A и Y A направлены противоположно силам, показан­ным на рис. 19.

Пример 8. Жесткая рама А BCD (рис.20) имеет в т. А неподвижную шарнирную опору, а т. D прикреплена к невесомому стержню. В т. С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р =20 кН. На раму действует пара силс моментомМ = 75 кНм и две силы F 1 =10 кН и F 2 =20 кН, составляющие со стержнями рамы углы =30 0 и =60 0 соответственно. При определении размеров рамы принять a =0,2 м. Определить реакции связей в точках А и D , вызванные действием нагрузки.

Дано : Р =20 кН, М =75 кНм , F 1 =10 кН, F 2 =20 кН, =30 0 , =60 0 , =60 0 , a = 0,2 м.

Определить: Х А, У А, R D .

Рис. 20

Указания. Задача – на равновесие тела под действием произвольной плоской системы сил. При ее решении следует учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы часто удобно разложить ее на составляющие и , для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда

Решение.

1.Рассмотрим равновесие рамы. Проведем координатные оси х, у и изобразим действующие на раму силы: силы и , пару сил с моментом М, натяжение троса (по модулю Т = Р) и реакции связей (реакцию неподвижной шарнирной опоры А представляем в виде составляющих; стержневая опора препятствует перемещению т. D рамы в направлении вдоль стержня,поэтомувтомженаправлениибудетдействоватьи реакция опоры ).

2. Составим уравнения равновесия рамы. Для равновесия произвольной плоской системы сил достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей и алгебраическая сумма моментов всех сил относительно любой точки на плоскости равнялись нулю.

При вычислении моментов сил и относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие , ; , и учтем, что .

Получим:

Подставив в составленные уравнения числовые значения заданных величин, и решив эти уравнения, определим искомые реакции.

Из уравнения (3) определяем R D =172,68 кН.

Из уравнения (1) определяем Х А = -195,52 кН.

Из уравнения (2) определяем У А = -81,34 кН.

Знаки «- » при величинах Х А и У А означают, что истинное направление этих реакций противоположно указанному на рисунке.

Проведемпроверку.

т. к. , то реакции опор найдены правильно.

Ответ: Х А = -195,52 кН, У А = -81,34 кН , R D = 172,68 кН.

Пример 9. Конструкция (рис. 21) состоит из жесткого угольника и стержня, которые в точке С свободно опираются друг о друга. Внешними связями, наложенными на конструкцию, являются: в точке А – жесткая заделка, в точке В – шарнир. На конструкцию действуют: пара сил с моментом М =80 кН·м, равномерно распределенная нагрузка интенсивности q =10 кН/м и силы: =15 кН и =25кН. При определении размеров конструкции принять а =0,35 м. Определить реакции связей в точках А, В и С.

Дано: М =80 кН·м, q =10 кН/м, F 1 =15 кН, F 2 =25 кН, а =0,35 м.

Определить: R A , M A , R B , R C .

Указания. Задача – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении можно или рассмотреть сначала равновесие всей системы, а затем равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, следует учесть, что ее реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой также неизвестен.

Решение.

в ыполняем его в соответствии с изложенной выше методикой.

1. В данной задаче изучается равновесие системы, состоящей из жесткого угольника и стержня.

2. Выбираем систему координат ХАУ (см. рис. 21).

3. Активными нагрузками на данную систему являются: распределенная нагрузка интенсивностью q , , и момент М.

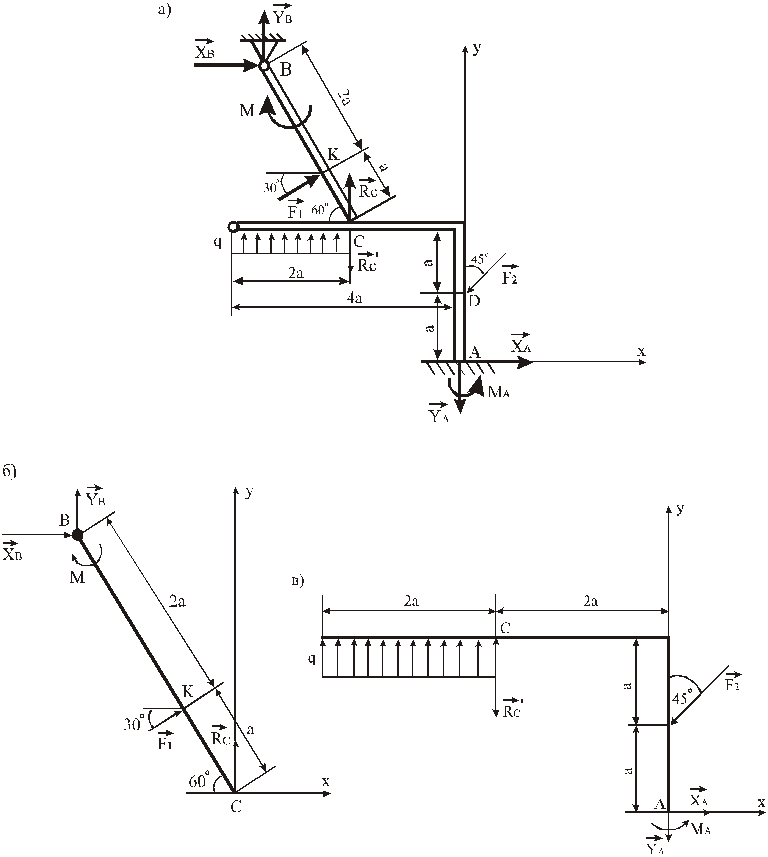
Рис.21

Изобразим на чертеже предполагаемые реакции связей. Так как жесткая заделка (в сечении А ) препятствует перемещению этого сечения стержня вдоль направлений Х и У , а также повороту стержня вокруг точки А , то в данном сечении в результате действия заделки на стержень возникают реакции , , . Шарнирная опора в точке В препятствует перемещению данной точки стержня вдоль направлений Х и У . Следовательно, в точке В возникают реакции , и . В точке С опоры стержня на угольник возникают реакция действия угольника на стержень и реакция действия стержня на угольник. Эти реакции направлены перпендикулярно плоскости угольника, причем R C = R ¢ С (согласно закону о равенстве действия и противодействия).

1. Задачу решаем способом расчленения. Рассмотрим сначала равновесие стержня ВС (рис. 21, б ). На стержень действуют реакции связей , , , сила и момент. Для полученной плоской системы сил можно составить три уравнения равновесия, при этом сумму моментов внешних сил и реакций связей удобнее считать относительно точки В :

;;(1)

;; (2)

Из уравнения (3) получим: R c =132,38 кН.

Из уравнения (1) получим: Х В = -12,99 кН.

Из уравнения (2) получим: У В = -139,88 кН.

Реакция шарнира в точке В:

Теперь рассмотрим равновесие угольника СА (рис. 21, в ). На угольник действуют: реакции связей , сила q . Заметим, что R / C = R C =132,38 кН. Для данной плоской системы сил можно составить три уравнения равновесия, при этом сумму моментов сил будем считать относительно точки С:

;;(4)

Из уравнения (4) получим: Х А = 17,75 кН.

Из уравнения (5) получим: У А = -143,13 кН.

Из уравнения (6) получим: М А = -91,53 кНм.

Задача решена.

А теперь для наглядного доказательства того, какое значение имеет правильный выбор точки, относительно которой составляется уравнение моментов, найдем сумму моментов всех сил относительно точки А (рис. 21, в ):

Из этого уравнения легко определить М А:

М А = -91,53 кНм.

Конечно, уравнение (6) дало то же значение М А, что и уравнение (7), но уравнение (7) короче и в него не входят неизвестные реакции Х А и У А, следовательно, им пользоваться удобнее.

Ответ: R A =144,22 кН, M A = -91,53 кНм, R B =140,48 кН,R C =R ¢ C =132,38 кН.

Пример 10 . На угольник АВС (), конец А которого жестко заделан, в точке С опирается стержень DE (рис. 22, а ). Стержень имеет в точке D неподвижную шарнирную опору, и к нему приложена сила , а к угольнику - равномерно распределенная на участке q и пара с моментом М .

Рис. 22

Д а н о: F =10 кН,М =5 кНм,q = 20 кН/м,а =0,2 м.

О п р е д е л и т ь: реакции в точках А , С , D , вызванные заданными нагрузками.

Указания. Задача - на равновесие системы тел, находящихся под действием плоской системы сил. При её решении можно или рассмотреть сначала равновесие всей системы в целом, а затем - равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учитывая при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, учесть, что её реакция представляется силой, модуль и направление которой неизвестны , и парой сил, момент которой тоже неизвестен.

Решение. 1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE (рис. 22, б ). Проведем координатные оси XY и изобразим действующие на стержень силы: силу , реакцию , направленную перпендикулярно стержню и составляющие и реакции шарнира D . Для полученной плоской системы сил составляем три уравнения равновесия:

,;( 1)